Uma parede cilíndrica é composta de dois materiais de condutividades térmicas e que são separados por um aquecedor elétrico delgado, para o qual as resistências de contato na interface são desprezíveis.
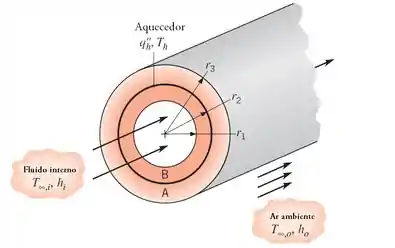
O líquido bombeado através do tubo encontra-se a uma temperatura e fornece um coeficiente de convecção na superfície interna da composição. A superfície externa é exposta ao ar ambiente, que está a e fornece um coeficiente de convecção . Em condições de regime estacionário, um fluxo de calor uniforme é dissipado pelo aquecedor.
Esboce o circuito térmico equivalente do sistema e expresse todas as resistências em termos das variáveis relevantes.
Obtenha uma expressão que pode ser utilizada para determinar a temperatura do aquecedor ().
Obtenha uma expressão para a razão entre os fluxos de calor para os fluidos interno () e externo (). Como as variáveis do problema podem ser ajustadas para minimizar essa razão?
Passo 1
Esboce o circuito térmico equivalente do sistema e expresse todas as resistências em termos das variáveis relevantes.
Como a gente já tá acostumado, bora fazer o circuito térmico. Para os sistemas radiais (cilindros e esferas), a gente só precisa fazer o circuito do centro pra fora, porque é simétrico pro outro lado!
Identificando as temperaturas em cada superfície (nós do circuito) e desenhando as resistências entre elas, a gente fica com:
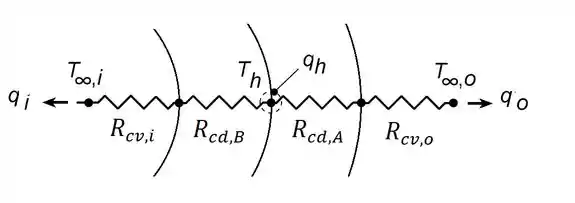
Como sabemos, as expressões de resistência térmica de convecção são as mesmas no caso de placa plana, cilindros ou esferas, o que muda é o cálculo da área de troca térmica ().
Para o caso acima, teremos:
Expressando as áreas em termos dos raios, temos que:
Mas a gente não conhece o comprimento do cilindro, e agora? Nem precisa, a gente pode simplesmente expressar as resistências relativas ao comprimento do cilindro:
“Show! Mas e as resistências de condução?” Ah, essas daí são diferentes do caso da parede plana e também diferem dos casos da esfera. Para corpos cilíndricos, a gente viu que:
Então, escrevendo as resistências térmicas de condução nas cascas cilíndricas e , a gente fica com:
Pela mesma estratégia que fizemos com as resistências de convecção, ficamos com:
Agora a gente já pode desenhar o circuito com as respectivas resistências em termos dos parâmetros relevantes do problema:

Passo 2
Obtenha uma expressão que pode ser utilizada para determinar a temperatura do aquecedor ().
Agora a gente precisa calcular a temperatura do aquecedor. Para isso, a gente pode tentar fazer o balanço de energia no ponto referente ao aquecedor!
Pelo circuito a gente pode ver que uma certa energia entra pelo ponto aquecedor e que ela vai se dissipar por dois caminhos diferentes ( e ). Como o enunciado dá os fluxos de saída por unidade de comprimento, para igualar entrada e saída precisamos multiplicar pelo perímetro do cilindro .
Sendo assim:
OBS: Se você achar essa forma muito complicada, você pode fazer o balanço na forma de taxa de calor (e não por fluxo), daí você vai ver que o comprimento vai cancelar em todos os termos da equação!
Continuando com a equação, a gente pode substituir as expressões dos calores:
Agora é álgebra, acabou a Transferência de Calor! A gente só tem que isolar a temperatura da equação. Então, bora lá!
Colocando a temperatura em evidência, a gente fica com:
E finalmente:
Passo 3
Obtenha uma expressão para a razão entre os fluxos de calor para os fluidos interno () e externo (). Como as variáveis do problema podem ser ajustadas para minimizar essa razão?
A razão entre os calores () é dada por:
Substituindo as expressões de e de , a gente fica com:
Para minimizar essa razão, a gente precisa diminuir os termos do numerador e/ou aumentar aqueles do denominador. De maneira, prática podemos:
- Aquecer o fluido que passa pelo interior (aumenta )
- Resfriar o fluido que passa pelo interior (diminui )
- Aumentar a velocidade do fluido no interior (aumenta )
- Aumentar a espessura da casca cilíndrica (aumenta )
- Diminuir a espessura da casca cilíndrica B (diminui )
Entre outras modificações quanto aos materiais e os fluidos.
Resposta

E as possíveis modificações para diminuir seu valor são listadas abaixo:
- Aquecer o fluido que passa pelo interior (aumenta )
- Resfriar o fluido que passa pelo interior (diminui )
- Aumentar a velocidade do fluido no interior (aumenta )
- Aumentar a espessura da casca cilíndrica (aumenta )
- Diminuir a espessura da casca cilíndrica B (diminui )