Existe a possibilidade de que no caso de uma tubulação, aumente-se a espessura de um certo isolante e isso aumente a transferência de calor ao invés de diminuir, tal como seria desejado ao aumentar a espessura de qualquer isolante. Isso nunca acontece quando a geometria é uma placa plana.
Explique o porquê, justificando MATEMATICAMENTE a sua resposta.
Passo 1
Isso pode acontecer porque, embora o isolante acrescente uma resistência térmica proporcional à espessura do isolante, a área externa também aumenta, aumentando a transferência de calor por convecção com o ambiente.
Vamos utilizar as seguintes variáveis pra resolver o problema:
- : Taxa de transferência de calor;
- : Temperatura na superfície interna do isolante;
- : Temperatura do ambiente;
- : Resistência térmica do isolamento;
- : Resistência térmica de convecção;
- : Raio externo do isolante;
- : Raio da superfície interna do isolante;
- : Coeficiente convectivo entre o tubo e o ambiente;
- : Comprimento do tubo.
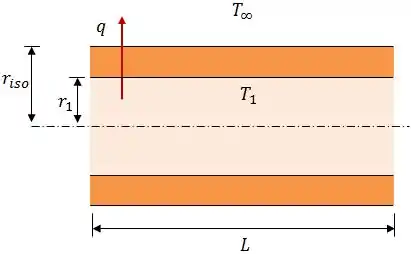
A taxa de transferência de calor pode ser escrita em função das resistências térmicas da seguinte forma:
Passo 2
Como estamos trabalhando com uma superfície cilíndrica, a resistência térmica de isolamento e a resistência térmica de convecção serão:
Assim, a taxa de transferência de calor será:
Supondo todos os parâmetros fixos, exceto o raio externo de isolamento , haverá um valor para o qual o isolamento deixará de reduzir a transferência de calor e vai passar a aumentar a transferência de calor.
Esse valor pode ser obtido se derivarmos a expressão da taxa de transferência de calor em relação a e igualarmos a zero.
Derivando a expressão de em relação a , teremos:
Analisando a expressão acima, veremos que ela será nula se:
Reorganizando a equação:
Esse será o raio crítico de isolamento.
![]()
Ou seja, caso , o isolante irá aumentar a transferência de calor. Mas se , o isolante irá reduzir a transferência de calor.
Resposta
Caso , o isolante irá aumentar a transferência de calor. Mas se , o isolante irá reduzir a transferência de calor.