Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Condução em Sistemas Radiais

Ver Teoria
Exercício 213456789101112

Enunciado

Um reservatório esférico D i n t = 0,8   m armazena um gás a temperatura de 240   ° C . A parede do reservatório é composta de aço ( k = 45   W / m K ) e tem uma espessura igual a 2   c m .

Deseja-se adicionar um material isolante, de forma a reduzir a perda de calor do reservatório em 50 % . Determine a espessura necessária de isolante, considerando que a sua condutividade térmica vale 0,04   W / m K . Considere o coeficiente de troca de calor interno igual a 5   W / m 2 K , e o externo igual a 25   W / m 2 K , e temperatura ambiente de 20   ° C .

Passo 1

Antes de colocar o isolante, o circuito térmico é dado por:

Onde:

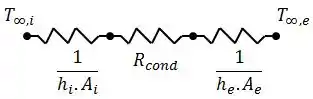
R t , c o n d = 1 4 . π . k   1 r i - 1 r e

Assim, a taxa de transferência de calor sem o isolante é dada por:

q = T ∞ , i - T ∞ , e R t

Onde a resistência térmica é dada por:

R t = 1 h i . A i + 1 4 . π . k   1 r i - 1 r e + 1 h e . A e

Trocando A pela área da superfície da esfera ( 4 . π . r 2 ) e substituindo os valores que temos:

R t = 1 5 . ( 4 . π . 0 , 4 2 ) + 1 4 . π . 45   1 0,4 - 1 0,42 + 1 25 . ( 4 . π . 0 , 42 2 )

R t = 0 , 1177   K / W

Assim, a taxa de transferência de calor sem o isolante é dada por:

q = 240 - 20 0 , 1177

q = 1869,2   W

Passo 2

Ao colocar o isolante, a taxa de transferência de calor será a metade, logo:

q ' = 0,5 . q → q ' = 934,6   W

Agora, como o isolante é colocado sobre a superfície externa da esfera, a resistência térmica equivalente será dada por:

R t ' = R t + R i s o = R t + 1 4 . π . k i s o   1 r e - 1 r i s o

Repare que:

r e = D i n t 2 + e s p e s s u r a = 0,42   m

Logo:

R t ' = 0,03 + 1 4 . π . 0,04 . 1 0,42 - 1 r i s o

R t ' = 0,03 + 4,74 - 2 r i s o

R t ' = 4,77 - 2 r i s o

Assim, o raio externo do isolante será:

q ' = T ∞ , i - T ∞ , e R t '

934,6 = 240 - 20 4,77 - 2 r i s o

4,77 - 2 r i s o = 0 , 2354

2 r i s o = 4 , 5346

r i s o = 0,4 4   m

Passo 3

Assim, a espessura do isolante será:

t i s o = r i s o - r e = 0,4 4 - 0,420

t i s o = 0 , 02   m

Resposta

t i s o = 0,0 2   m

Exercícios de Livros Relacionados

Considere um tubo a uma temperatura constante cujo raio seja maior que o raio crítico de isolamento. Alguém alega que a taxa de perda de calor do tubo aumentou quando algum isolamento é adicionado ao
Um tanque esférico de 50 cm de diâmetro está cheio com água com gelo a 0 °C. O reservatório é de casca fina, e a temperatura pode ser considerada a mesma temperatura do gelo. O reservatório é exposto
Tubos de cobre estão fixados à placa absorvedora de um coletor solar plano, conforme mostrado na figura.A placa absorvedora feita com a liga de alumínio (2024-T6) possui 6 mm de espessura e é isolada
Um motor recebe potência elétrica P e l e de uma linha de força e transmite potência mecânica P m e c para uma bomba através de um eixo rotativo de cobre com condutividade térmica k e , comprimento L
Tubos de cobre estão fixados a uma placa de um coletor solar, com espessura t, e o fluido de trabalho mantém a temperatura da placa acima dos tubos em Te. Há um fluxo térmico radiante líquido uniforme