Rejeitos radioativos são colocados em um recipiente esférico de parede delgada. Os rejeitos geram energia térmica por unidade de volume . O raio do recipiente é .
Assumindo que o recipiente está inicialmente a uma temperatura e sabendo que esse é colocado em um líquido inerte que se encontra a e que fornece um coeficiente convectivo uniforme.
Determine o comportamento da temperatura com o tempo no interior do recipiente.
Qual a temperatura do estado estacionário?
Determine a quantidade de calor trocada com o meio após atingir o estado estacionário.
Para todos os casos assuma modelo de parâmetros concentrados.
Expresse os resultados em termos de , , , , (condutividade térmica do rejeito), (massa específica) e (capacidade térmica do rejeito).
Passo 1
Determine o comportamento da temperatura com o tempo no interior do recipiente.
Utilizando o método dos parâmetros concentrados, fazendo o balando de energia no recipiente, teremos o seguinte:
Como não há energia entrando no recipiente:
Repare que, como temos um termo de geração de energia, não podemos usar a solução já dada pelo método dos parâmetros concentrados. Ou seja, teremos que resolver essa equação diferencial pra encontrar a temperatura em função do tempo.
Passo 2
Essa equação diferencial é separável. Assim, vamos arrumá-la separando a derivada do resto da equação.
Onde corresponde ao volume da esfera, e corresponde à área superficial. Assim, a razão será:
Assim:
Separando a temperatura do tempo, teremos:
Integrando dos dois lados:
Passo 3
O lado direito pode ser integrado usando o método da substituição, onde:
Logo:
Agora é só arrumar a bagunça:
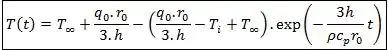
Passo 4
Qual a temperatura do estado estacionário?
A temperatura do estado estacionário é dada para . Assim:
![]()
Passo 5
Determine a quantidade de calor trocada com o meio após atingir o estado estacionário.
A quantidade de calor trocada com o meio é dada por:
Substituindo a expressão que encontramos na letra :
Onde .
![]()
Ou seja, no estado estacionário, a quantidade de calor trocada com o meio será igual à quantidade de calor gerada pelo rejeito radioativo.
Resposta