A medida que as estações espaciais permanentes aumentam de tamanho, existe um consequente aumento na quantidade de potência elétrica que elas dissipam. Para manter a temperatura nos compartimentos internos dentro de limites estabelecidos, torna-se necessário transferir o calor dissipados para o espaço.
Um novo sistema proposto para a dissipação de calor é conhecido por Radiador de Gotículas Líquidas. O calor é incialmente transferido para um óleo especial para alto vácuo, que é então injetado no espaço exterior em forma de uma corrente de pequenas gotículas. A corrente percorre uma distância , ao longo da qual se resfria pela irradiação de energia para o espaço exterior, que se encontra a uma temperatura absoluta igual a zero. As gotículas são, então, coletadas e retornadas para a estação espacial.
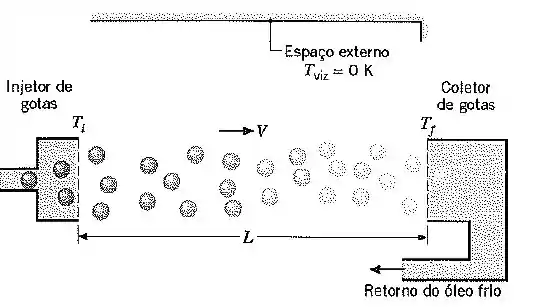
Considere condições nas quais as gotas, com emissividade e diâmetro , são injetadas no espaço a uma temperatura e a uma velocidade .
As propriedades do óleo são , e .
Supondo que cada gota irradia calor para o espaço externo a , determine a distância necessária para que as gotículas atinjam o coletor a uma temperatura final . Qual é a quantidade de energia térmica dissipada por cada gota?
Passo 1
Vamos nessa! Logo de cara temos que calcular o número de Biot pra sabermos qual método utilizaremos pra resolver essa bagaça.
Tratando as gotículas como esferas perfeitas, o comprimento característico é dado por . Além disso, como a gotícula está perdendo calor por radiação, no lugar de , utilizaremos que é o coeficiente de transferência de calor por radiação. Dessa forma:
Onde:
Substituindo os valores:
Passo 2
Se esse fosse um problema de convecção, bastaria utilizar as equações que usamos até aqui. Mas como estamos tratando de um problema com radiação, vamos ter que voltar um pouquinho.
Se liga! Se fizermos um balanço de energia para a nossa gotícula, veremos que:
Onde , logo:
Reorganizando e integrando a equação, teremos:
Agora sim estamos prontos pra seguir em frente! :)
Passo 3
O problema nos deu que:
Substituindo os valores:
Passo 4
Já calculamos quanto tempo leva para a gotícula chegar à temperatura de , mas estamos preocupados em saber a distância que a mesma percorre até que isso aconteça.
Como as partículas foram injetadas com uma velocidade constante , podemos calcular a distância da seguinte forma:
Passo 5
Pra terminar (juro), queremos saber a quantidade de energia dissipada por cada gota.
Essa quantidade de energia é justamente a quantidade de energia que a gota perdeu para a vizinhança, logo:
Substituindo os valores:
ACABOU!
