Uma esfera sólida de aço () de de diâmetro é revestida com uma camada de material dielétrico de espessura e condutividade térmica . A esfera revestida está inicialmente a uma temperatura de e é subitamente resfriada em um grande banho de óleo, o qual se encontra a e . Estime o tempo necessário para que a temperatura da esfera revestida atinja .
Dica: despreze o efeito do armazenamento de energia no material dielétrico, uma vez que sua capacidade térmica () é pequena quando comparada com a da esfera de aço.
Passo 1
Esse é exatamente pra gente exercitar e ver se entendemos tudo certinho! Bora lá!
A situação proposta pelo enunciado pode ser esquematizada da seguinte forma:
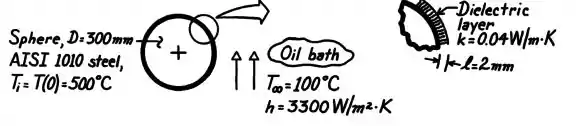
Bom, então a gente tem que calcular quanto tempo leva pra esfera atingir . Como é um problema transiente, a gente pode verificar se dá pra usar o método dos parâmetros concentrados
Então, bora calcular o número de Biot desse problema:
Mas aqui a gente não tem só a esfera, tem também um revestimento que a gente precisa contabilizar! Mas tem uma forma da gente simplificar isso, dá uma olhada!
A gente sabe que uma esfera aquecida sem isolamento vai perder calor para o fluido e essa transferência está associada à resistência de convecção do meio. Se colocarmos um revestimento, essa resistência à transferência aumenta e passa a ser:
Substituindo as expressões da resistência convectiva e condutiva na esfera:
Mas por que estamos fazendo isso? Porque a gente precisa de uma expressão para o coeficiente de convecção () pra calcular o , mas não podemos usar o direto, porque temos que levar em consideração a resistência do revestimento.
Agora que a gente já sabe a resistência, podemos propor um coeficiente global de transferência (), que contabiliza os dois efeitos (condução e convecção) da seguinte forma:
Dividindo pela área da esfera, a gente fica com o coeficiente global:
A gente deve calcular o com esse valor!
Passo 2
Além disso, o comprimento característico () pode ser calculado de duas maneiras:
- Razão entre o volume do sólido e a área superficial do sólido.
- Comprimento correspondente à maior diferença de temperatura no sólido.
Bora ver quanto dá cada um deles. Pela razão entre volume e área da esfera, a gente fica com:
Pela distância que corresponde a maior diferença de temperatura, a gente tem que:
Como o fica menor usando a primeira opção, bora usar ele, porque assim fica mais fácil da aproximação do método dos parâmetros concentrados valer ^^
Assim:
Como , a gente pode usar o método dos parâmetros concentrados! Então, vamos aos cálculos!
Passo 3
O enunciado é um exemplo do caso A, então temos que:
Podemos escrever de outra forma:
Substituindo os valores do enunciado:
Isso equivale a aproximadamente !