Um armazenamento de energia térmica consiste em um grande canal retangular no qual é bem isolado em sua superfície externa e engloba camadas alternadas de material de armazenagem e canal de escoamento.
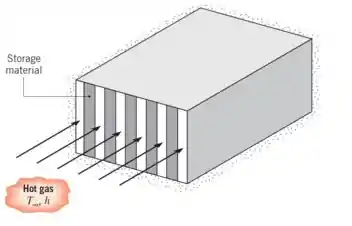
Cada camada do material de armazenamento é uma placa de alumínio () de largura , a qual está a uma temperatura de . Considere condições para as quais a unidade de armazenamento é carregada pela passagem de um gás quente através dos canais. A temperatura do gás e o coeficiente de convecção são considerados valores constantes de e em todo o canal.
Quanto tempo irá levar para atingir da energia armazenada máxima possível?
Qual será a temperatura do alumínio nesse instante?
Passo 1
Quanto tempo irá levar para atingir da energia armazenada máxima possível?
A gente pode encarar o problema como sendo várias paredes planas, tais que:
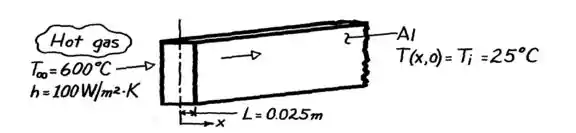
Dessa maneira, a gente precisa calcular o número de Biot do bloco pra verificar a validade da aproximação do método dos parâmetros concentrados ().
Para o caso das paredes planas, o comprimento característico () é exatamente a metade da largura da parede (), então:
Substituindo os valores:
Como , a gente pode usar o método dos parâmetros concentrados!
Passo 2
O enunciado nos pede qual é o tempo () pra que a quantidade de energia armazenada atinja da quantidade máxima de calor (). A gente pode escrever da seguinte maneira:
A gente sabe que a quantidade de calor na situação do corpo sob convecção somente depende do tempo e é dada por:
Vamos entender então o que acontece em diferentes momentos:
No instante inicial, a transferência de calor ainda não começou, logo a quantidade de calor trocado será igual a zero, como podemos ver substituindo na equação:
Daí pra frente, quanto maior o valor de , menor será o valor da exponencial e consequentemente maior será a quantidade de energia trocada. Sendo assim, o máximo de calor trocado é atingido quando o tempo tender ao infinito:
Substituindo na equação:
Assim:
Em que:
Logo:
Isso significa aproximadamente .
Passo 3
Qual será a temperatura do alumínio nesse instante?
Agora estamos num problema do caso B, em que já sabemos o tempo () e precisamos determinar a temperatura do corpo! Sendo assim, a gente tem que:
Substituindo os valores que encontramos e já sabemos do enunciado:
Logo:
E, lembrando da definição da temperatura de excesso, a temperatura da esfera nesse instante será:
Resposta