Um arame longo de diâmetro é imerso em um banho de óleo à temperatura de . O arame possui uma resistência elétrica por unidade de comprimento de . A corrente que flui através do arame vale , o coeficiente de convecção é e as propriedades do arame são ,, .
Qual é a temperatura em regime estacionário do arame?
A partir do tempo em que a corrente é aplicada, quanto tempo levará para o arame atingir uma temperatura que não exceda do valor do regime estacionário?
Passo 1
Qual é a temperatura em regime estacionário do arame?
A situação pode ser esquematizada da seguinte forma:
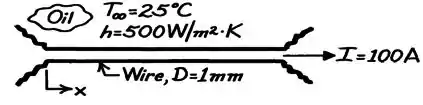
O item a) nos pede pra calcular a temperatura em estado estacionário, então não temos que usar ainda nenhum dos métodos de condução transiente.
A gente observa que há geração de energia térmica no corpo, devido à passagem de corrente elétrica no arame. Então, bora fazer o que a gente já tava acostumado para os casos de estado estacionário: um balanço de energia!
A taxa de calor gerada () se refere ao efeito Joule pela dissipação da energia elétrica em térmica e a taxa de saída () é dada pela convecção na superfície.
Como a resistência elétrica é dada em termos do comprimento do fio, a gente pode escrever a área também dividida pela unidade de comprimento ():
Isolando a temperatura da superfície:
Substituindo os valores do enunciado:
Passo 2
A partir do tempo em que a corrente é aplicada, quanto tempo levará para o arame atingir uma temperatura que não exceda do valor do regime estacionário?
A primeira coisa que temos que fazer é calcular o número de Biot pra saber se podemos usar o Método dos Parâmetros Concentrados:
O comprimento característico () pela razão entre volume e área do cilindro é calculado por:
Pela distância que corresponde a maior diferença de temperatura, a gente tem que:
Como o fica menor usando a primeira opção, bora usar ele, porque assim fica mais fácil da aproximação do método dos parâmetros concentrados valer ^^
Assim:
Como , a gente pode usar o método dos parâmetros concentrados! Então, vamos aos cálculos!
Passo 3
Esse exemplo aqui é um pouco diferente, porque tem geração de energia térmica devido à passagem de corrente elétrica no arame.
O Então, bora fazer um balanço de energia transiente nesse corpo:
OBS: Como o termo de geração não é nulo, a gente não pode utilizar aquelas equações prontas que vimos na teoria, porque elas só servem pro caso trivial de saída de calor por convecção!
Substituindo as expressões:
Isolando a derivada da temperatura no tempo:
Dividindo por “” e reorganizando:
Agora a gente pode fazer a seguinte mudança de variável:
Assim:
Integrando a equação desde o tempo inicial () até um instante qualquer:
Reorganizando:
Voltando para as variáveis convencionais (expressão para ):
Substituindo os valores do enunciado:
Aplicando o logaritmo natural na equação: