Uma parede plana de um forno é fabricada de aço carbono (,, ) com espessura . A fim de proteger a parede dos efeitos da corrosão dos gases de combustão do forno, uma superfície da parede é revestida com um fino filme de cerâmica, para uma unidade de área superficial, tem uma resistência térmica de . A superfície oposta é bem isolada do ambiente.
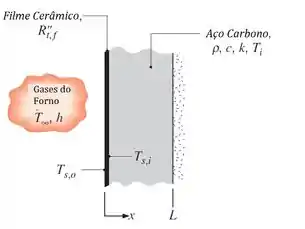
Quando o forno entra em operação, a parede encontra-se a uma temperatura inicial de e os gases de combustão a entram no forno, promovendo um coeficiente de convecção de no filme cerâmico.
Considerando que a capacidade térmica do filme é desprezível, quanto tempo levará para a superfície interna do aço atingir a temperatura de ?
Qual é a temperatura da superfície exposta do filme cerâmico nesse instante?
Passo 1
Se a gente olhar rápido pra situação proposta acima, a gente vai achar que não dá pra usar o método dos parâmetros concentrados. Isso porque, pra usar o método, o sólido tem que estar sujeito à convecção em todos os lados.
No caso da parede plana, as duas faces devem estar sob fenômenos de convecção e, nesse exercício, nenhum dos lados tá nessa situação! Dá uma olhada:
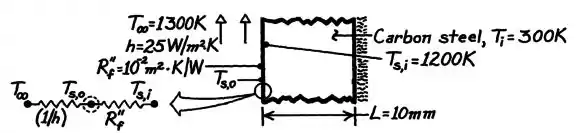
Do lado esquerdo, a gente tem o filme cerâmico, oferecendo uma resistência adicional à transferência de calor. Mas isso a gente já viu antes! A gente pode calcular a resistência global e determinar um coeficiente global de troca térmica ().
Mas lado direito, a superfície tá isolada! Não dá pra usar essa estratégia! Pra resolver isso, a gente pode lembrar de algo que aprendemos bem lá no comecinho:
“Para resolver paredes planas com condições de contorno simétricas, basta resolver um dos lados, considerando no meio da placa fluxo zero.”
Então, a gente vai fazer ao contrário: como aqui a gente tem “metade” de uma parede plana (), a gente vai resolver como se fosse uma parede completa, porque dá no mesmo, devido à simetria!
Passo 2
Considerando que a capacidade térmica do filme é desprezível, quanto tempo levará para a superfície interna do aço atingir a temperatura de ?
A primeira coisa que temos que fazer é o que mesmo? Isso! Calcular o número de Biot:
Em que o comprimento característico () para paredes planas de comprimento é exatamente . Como estamos assumindo que a situação é metade de uma parede plana, então mesmo!
Agora o coeficiente de convecção não será o , porque temos que considerar ainda a resistência do filme cerâmico. Sendo assim, a gente precisa determinar o coeficiente global de transferência ().
A resistência total é dada por:
Como, na parede plana, o fluxo de calor é constante (já que a área é constante), a gente pode trabalhar direto com as resistências :
Substituindo a expressão da resistência convectiva:
Logo, o coeficiente global () será:
Assim o número de Biot () será:
Como , a gente pode usar o método dos parâmetros concentrados!
Passo 3
A gente precisa achar o tempo necessário para que a temperatura alcance , então esse é o caso A. Sendo assim, a gente tem que:
Substituindo os valores:
Isso equivale a aproximadamente .
Passo 4
Qual é a temperatura da superfície exposta do filme cerâmico nesse instante?
Nesse instante, a gente sabe que a temperatura da superfície interna do aço vale . A gente pode aplicar a estratégia do circuito térmico pra determinar a temperatura :
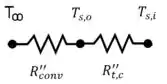
Assim:
Isolando a temperatura externa do filme cerâmico:
Substituindo os valores do enunciado: