Exercícios Resolvidos de Matriz que Representa uma TL

Ver Teoria

Exercício 22 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58

Enunciado

Sejam e . Considere o conjunto .

(a) Mostre que é base do .

(b) Determine e .

(c) Determine para .

(d) A projeção (não necessariamente ortogonal) de um vetor w sobre um vetor v, na direção de um vetor u, é o vetor w’ que tem a direção de v e tal que w-w’ tem a direção de u, como a figura abaixo.

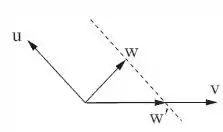
Encontre a matriz da transformação linear que é a projeção de (x,y) sobre na direção de .

Passo 1

(a) Pra ser base, o conjunto deve ser capaz de gerar todo o espaço e ser LI.

A dimensão de é 2, então com no mínimo dois vetores conseguimos gerar esse espaço.

Agora precisamos mostrar que e são LI.

Como só temos dois vetores, para eles serem LI basta que um não seja múltiplo do outro.

Vemos que e não são múltiplos, logo não são combinação linear um do outro e o conjunto é LI.

Então, é base de .

Passo 2

(b) Para escrever um vetor em uma base, precisamos encontrar as coordenadas dele nessa base.

Então, para o vetor (1,0) na base , vamos precisar achar os valores de a e b tais que:

Vamos ficar com o sistema:

Pela segunda equação:

Substituindo na primeira:

Então:

E o vetor (1,0) na base vai ser:

Fazendo a mesma coisa pro vetor (0,1), queremos encontrar c e d tais que:

Temos o sistema:

Pela primeira equação:

Substituindo na segunda:

Logo:

E o vetor (0,1) na base vai ser:

Passo 3

No primeiro caso, temos a primeira coluna da matriz de mudança de base de para a base canônica do .

No segundo, temos a segunda coluna dessa matriz.

Ela vai ser então:

Aplicando A a um vetor (x,y) qualquer do , vamos ter:

Logo:

Passo 4

(d) A projeção definida no enunciado faz com que os vetores que estão na direção de permaneçam iguais, enquanto os que estão na direção de sejam zerados.

Logo, queremos encontrar uma matriz P para essa transformação tal que:

A primeira coluna dessa matriz P pode ser encontrada se aplicarmos o vetor (1,0) a ela.

Vimos antes, na letra (b), que o vetor (1,0) pode ser escrito como:

Aplicando P nos dois lados:

Como a transformação é linear, podemos fazer:

Como definimos P(2,1)=(2,1) e P(1,-3)=(0,0):

Essa é a primeira coluna de P!

Agora, pra achar a segunda coluna de P, aplicamos o vetor (0,1) a essa matriz.

Vimos também na letra (b) que o vetor (0,1) pode ser escrito como:

Aplicando P dos dois lados:

Como a transformação é linear, podemos fazer:

Usando o que definimos antes:

Acabamos de achar a segunda coluna de P!

Então, a matriz P vai ser:

Resposta

(b)

(c)

(d)

Exercícios de Livros Relacionados

Seja T o operador linear dado pela matriz: 1 2 - 1 2 0 1 1 - 2 2 a) Calcular N ( T ) e dim ⁡ N ( T ) . b) Calcular I m ( T ) e dim ⁡ I m ( T ) .

Seja o espaço vetorial V = M ( 2 ,2 ) e a transformação linear T : V → R 3 , T a b c d = ( a + b , c - d , 2 a ) a) Mostrar que T é linear.b) Determinar T B A sendo A e B as bases canônicas de M ( 2 ,

Consideremos as transformações lineares S e T de R 3 em R 2 definidas por S x , y , z = ( 2 x - y , 3 x - 2 y + z ) e T x , y , z = ( x + y - z , y - 2 z ) .a) Determinar o núcleo da transformação lin

As transformações S :R 2 → R 3 e T :R 3 → R 2 são tais que S x , y = ( y , x - y , 2 x + 2 y ) e T x , y , z = ( x , y ) .a) Sendo B = { 1 ,0 , - 1 ,1 ,1 ,1 ,1 ,0 ,0 } uma base do R 3 , determinar a m

Sendo S e T operadores lineares do R 3 definidos por S x , y , z = ( x ,2 y , x - y ) e T x , y , z = ( x - z , y , z ) , determinar:a) [ S ∘ T ] .b) [ T ∘ S ] .