Considere a transformação linear dada pela matriz
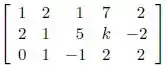
Onde k é uma constante real. Determine, se possível, o que é pedido abaixo em cada item.
Caso não seja possível, justifique.
(a) Todos os valores de k tais que
(b) Todos os valores de k tais que
(c) Todos os valores de k tais que
(d) Todos os valores de k tais que
Passo 1
A matriz para a transformação T dada foi:
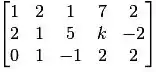
Vamos considerar essa matriz como sendo uma matriz formada pelos vetores u, v e w nas linhas, desse jeito:
Passo 2
Passo 3
(a) e (b)
O contradomínio da transformação T é .
Como a imagem mora no contradomínio, sua dimensão é menor ou igual a 3:
Lembra que a dimensão da imagem também é igual ao número de linhas LI?
Para que a dimensão da imagem seja 0, todas as 3 linhas teriam que ser LD, certo?
Mas os vetores u e w das linhas não são múltiplos, pois a primeira coordenada de u é um inteiro e a primeira de w é zero.
Então, a dimensão da imagem de T só pode ser 2 ou 3.
Passo 4
(c) Para que , a segunda linha da matriz T, isso é, o vetor v, teria que uma combinação linear de u e w.
Ou seja, teríamos que ter:
Da primeira coordenada, temos que:
Substituindo na terceira:
Substituindo esses valores na quarta coordenada:
Passo 5
(d) Vamos usar o raciocínio “contrário” da (c) aqui!
Queremos que a dimensão da imagem seja 3, então nenhuma das linhas vai poder ser CL de outra.
Como vimos que só era possível a segunda linha ser CL da primeira e da terceira, e a condição para isso era que:
Agora, para que isso não ocorra, vamos ter:
Ou seja, qualquer valor de é possível para que Dim(Im(T)) seja 3.
Resposta
(a) para todo k pois ou 3.
(b) para todo k pois ou 3.
(c)
(d) k qualquer, desde que