Seja a transformação linear que é a projeção ortogonal sobre o plano de equação

E seja a projeção afim que é a projeção ortogonal sobre um plano paralelo ao plano .

(a) Mostre que a transformação P é definida pela matriz:

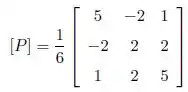
(b) Determine Im(P)

(c) Encontre uma base do espaço nulo de P

(d) Encontre, se houver, uma base de feita com vetores que sejam autovetores de P. Caso contrário, justifique.

(e) Nos itens seguintes, assuma que e determine:

e.1) A expressão para F, ou seja, determine F(x,y,z) (pode responder usando matrizes, se preferir)

e.2) A equação cartesiana do plano .

Se estamos projetando ortogonalmente no plano , então os vetores que estão nesse plano não vão ser alterados pela nossa matriz de projeção, certo?

Dois vetores que estão nesse plano são os vetores da base dele, que achamos no passo 1:

Então vamos ter:

Onde P é a matriz (ou transformação linear, como você preferir :D) que faz a projeção no plano.

Por outro lado, se temos um vetor perpendicular ao plano, então a projeção ortogonal dele no plano vai ser o vetor nulo, né?

Então como tínhamos o vetor normal

Vamos ter também que:

Agora vamos lembrar que pra encontrar a primeira, a segunda e a terceira coluna da matriz P, precisamos fazer, respectivamente:

Ou seja, precisamos dar um jeito de escrever os vetores (1,0,1), (0,1,0) e (0,0,1) a partir das informações que temos até agora, que são basicamente, a base dos vetores do plano

E a base do complemento ortogonal

Vamos começar com o vetor (1,0,0)!!

Vamos escrevê-lo como uma combinação linear dos três vetores que temos:

Resolvendo esse sistema, vamos encontrar:

Então:

Aplicando a transformação P dos dois lados:

Como a transformação é linear, podemos fazer:

Mas vimos antes que:

Loooogo, substituindo esses valores, vamos encontrar:

E essa é a primeira coluna da matriz P!

Agora vamos repetir todo esse processo pra achar a segunda coluna.

Vamos escrever o vetor (0,1,0) como uma combinação linear dos três vetores que temos:

Resolvendo esse sistema, vamos encontrar:

Então:

Aplicando a transformação P dos dois lados:

Como a transformação é linear, podemos fazer:

Substituindo aquelas relações que achamos antes, vamos ter a segunda coluna de P:

Por último, finalmente vamos achar a terceira coluna de P.

Vamos escrever o vetor (0,0,1) como uma combinação linear dos três vetores que temos:

Resolvendo esse sistema, vamos encontrar:

Então:

Aplicando a transformação P dos dois lados:

Como a transformação é linear, podemos fazer:

Substituindo aquelas relações que achamos antes, vamos ter a terceira coluna de P:

Então P vai ser a matriz:

Que é idêntica à matriz dada no enunciado! 😊

(b) Como a matriz P faz a projeção de vetores do sobre o plano , a imagem de P é o próprio plano

(c) O espaço nulo de P são os vetores que são zerados pela matriz P, isto é, são os vetores que são projetados em (0,0,0).

Lembra que vimos isso no passo 1??

Os vetores que são perpendiculares ao plano são levados no (0,0,0) e vimos que uma base pra esses vetores é:

(d) Vimos no passo 2 que:

Isso não te lembra aquela história de autovalor e autovetor??

Porque olha só, estamos dizendo que o vetor (1,0,1) aplicado a P resulta em 1 vez o próprio (1,0,1). Então, (1,0,1) é autovetor associado ao autovalor .

Seguindo o mesmo raciocínio, temos que (0,1,2) é autovetor associado a e que (1,2,-1) é autovetor associado a .

Logo, temos uma base:

Formada por três autovetores de P.

O espaço formado pelos três vetores dessa base tem dimensão 3 (os três vetores são LI), assim como o .

Logo,

É uma base de de feita com autovetores de P.

(e) Foi dito no enunciado que o plano é paralelo ao plano .

A equação do plano é:

A gente viu que o vetor normal desse plano é

Se dois planos são paralelos, eles têm o mesmo vetor normal.

Então a equação do plano vai ser do tipo:

(e.1) Foi dito no enunciado que F faz a projeção ortogonal sobre .

Então a imagem dos vetores projetados por F vai ser igual a imagem dos vetores projetados por P mais um termo que é dado pela “altura” do plano em relação ao plano , ou seja, F(0,0,0).

Temos então:

Como temos pelo enunciado que:

E vimos no passo 2 que:

Então:

Substituindo os valores de F(1,0,0) e P(1,0,0), vamos encontrar que:

Então:

Escrevendo a matriz P da letra (a) na forma de vetor, vamos ter:

Então:

(e.2) Como pertence a , vamos substituir o ponto na equação do plano que definimos no passo 6:

Logo a equação do plano vai ser: