G1 de Cálculo 1 - MAT1161 da PUCRIO - 2018.1

Seja uma função derivável definida no intervalo . O gráfico abaixo é o gráfico da derivada de , ou seja, o gráfico de :

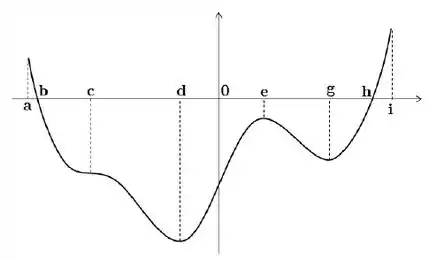
Decida se cada uma das afirmações abaixo é verdadeira ou falsa, justificando sua resposta

1. A reta tangente ao gráfico de em tem inclinação negativa

Seja uma função derivável definida no intervalo . O gráfico abaixo é o gráfico da derivada de , ou seja, o gráfico de :

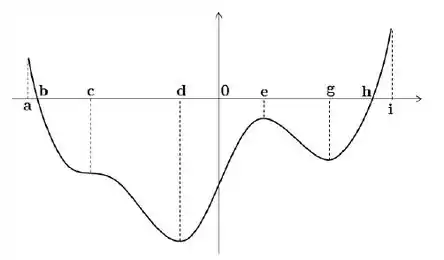
Decida se cada uma das afirmações abaixo é verdadeira ou falsa, justificando sua resposta

d) No intervalo o gráfico de é côncavo pra cima

Seja uma função derivável definida no intervalo . O gráfico abaixo é o gráfico da derivada de , ou seja, o gráfico de :

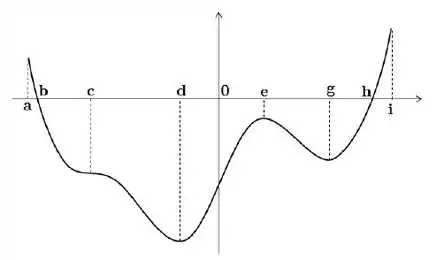
Decida se cada uma das afirmações abaixo é verdadeira ou falsa, justificando sua resposta

b) O ponto é um ponto de inflexão do gráfico de

Seja uma função derivável definida no intervalo . O gráfico abaixo é o gráfico da derivada de , ou seja, o gráfico de :

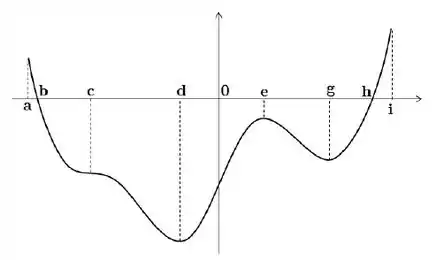
Decida se cada uma das afirmações abaixo é verdadeira ou falsa, justificando sua resposta

c) A função tem um mínimo local em

Sabendo que

É a equação de uma circunferência de centro e raio , considere a região plana

1. Esboce abaixo a região . Indique explicitamente em seu desenho as coordenadas de três pontos que pertençam à fronteira da região.
2. Calcule a área da região utilizando o método que preferir.

Considere a função dada por:

Determine caso exista(m):

(a.1) O(s) intervalo(s) de crescimento e decrescimento de

(a.2) O(s) valor(es) de para os quais a função possui máximo local e mínimo local.

(b.1) O(s) intervalo(s) onde o gráfico de tem concavidade voltada para cima e onde tem concavidade voltada para baixo.

(b.2) O(s) ponto(s) de inflexão do gráfico de .

(c) Faça um esboço do gráfico de indicando explicitamente o(s) ponto(s) de máximo, de mínimo e de inflexão determinado(s) nos itens anteriores. Esboce também a(s) reta(s) tangente(s) ao gráfico de no(s) ponto(s) em que a derivada é zero e no(s) ponto(s) de inflexão

(d) A equação sempre possui solução? Justifique sua resposta.