Seja uma função derivável definida no intervalo . O gráfico abaixo é o gráfico da derivada de , ou seja, o gráfico de :
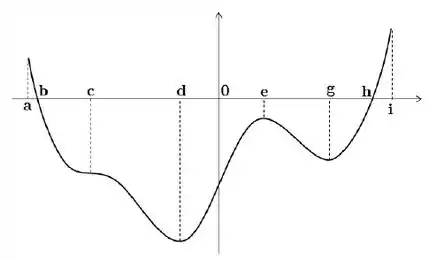
Decida se cada uma das afirmações abaixo é verdadeira ou falsa, justificando sua resposta
- A reta tangente ao gráfico de em tem inclinação negativa
Passo 1
Opa, vamos lá. Antes da gente mergulhar na questão vamos lembrar de uma coisa muito importante: o gráfico não é de e sim de . Como a equação da reta tangente é:
Sendo o ponto de tangência e a inclinação da reta tangente, basta a gente ver onde que o gráfico tá no nosso ponto! Show de bola:
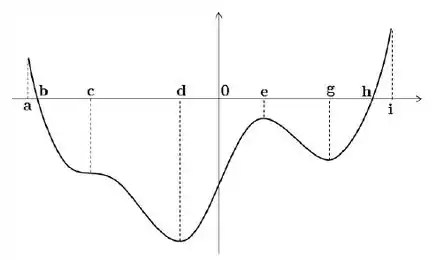
Do gráfico, quando , ! E taí! Como a primeira derivada é negativa no ponto em questão, então a inclinação da reta tangente vai ser negativa! Verdadeiríssima a questão!
Resposta
Verdadeiro, pois
Exercícios de Livros Relacionados
Quantas retas tangentes à curva y = x / ( x + 1 ) passam pelo ponto ( 1 ,2 ) ? Em quais pontos essas retas tangentes tocam a curva?
Se G x = 4 x 2 - x 3 , encontre G ' ( a ) e use-o para encontrar equações das retas tangentes à curva y = 4 x 2 - x 3 nos pontos ( 2 ,8 ) e ( 3,9 ) .Ilustre a parte (a) traçando a curva e as retas tan
Encontre uma equação da reta tangente à curva y = 2 1 + e - x no ponto 0,1 .Ilustre a parte (a) fazendo o gráfico da curva e da tangente na mesma tela.
Encontre a equação da reta tangente à curva no ponto dado y = x - 1 x - 2,( 3,2 )
Esboce o gráfico de uma função f para a qual f 0 = 0 ,f ' 0 = 3,f ' 1 = 0ef ' 2 = - 1