Seja uma função derivável definida no intervalo . O gráfico abaixo é o gráfico da derivada de , ou seja, o gráfico de :
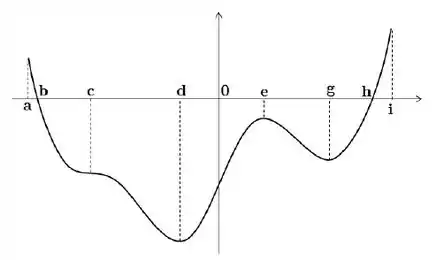
Decida se cada uma das afirmações abaixo é verdadeira ou falsa, justificando sua resposta
c) A função tem um mínimo local em
Passo 1
Beleza, a questão quer saber se é um ponto de mínimo. Bem, como um ponto de mínimo é um ponto crítico, ou seja, um ponto em que a inclinação da reta tangente dá , da equação da reta tangente, temos:
E logo:
Sendo o ponto de tangência. Saca só o gráfico agora:
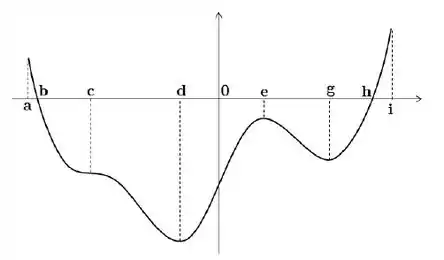
E olha só! Se , teremos de fato:
Então é sim um ponto crítico, mas seria ele de mínimo?
Passo 2
Pra gente ver se o é mesmo um ponto de mínimo, vamos lembrar de uma coisa:

E olha só, nesse caso, vamos ter que:
- Pouco depois de ,
- Pouco antes de ,
Puts, então se encaixa em um ponto de máximo e não de mínimo! A questão é falsa!
Resposta
Falsa! é um ponto de máximo