Seja uma função derivável definida no intervalo . O gráfico abaixo é o gráfico da derivada de , ou seja, o gráfico de :

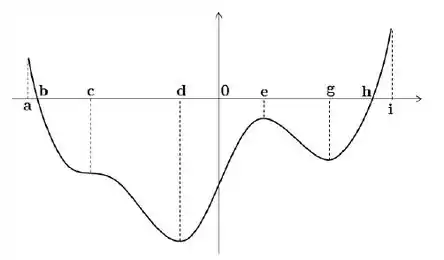
Decida se cada uma das afirmações abaixo é verdadeira ou falsa, justificando sua resposta

d) No intervalo o gráfico de é côncavo pra cima

Beleeza, vamos lá. A questão quer saber sobre a concavidade de . Bem, vamos precisar analisar a segunda derivada. Mas peraí, o gráfico:

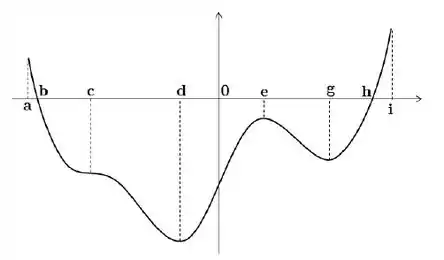
É da primeira derivada! E agora? Calma gafanhoto! A gente pode até não ter o gráfico de , mas olha só:

Se a segunda derivada é a derivada da primeira derivada, então a gente pode brincar de reta tangente aqui! Dá uma olhada em como vai ficar a equação da reta tangente ao gráfico de :

Onde é o ponto de tangência e a inclinação da reta tangente. Agora dá uma olhada no intervalo . Se dividirmos esse intervalo em dois:

Vamos poder analisar cada um desses dois intervalos. E puts, olha como fica a segunda derivada em cada um:

Se o sinal da segunda derivada está mudando a partir de , é porque é um ponto de inflexão.

A questão vai ser falsa então. Nem sequer temos um tipo de concavidade só no intervalo pra dizer que esse único tipo é virada pra cima!