Sabendo que
É a equação de uma circunferência de centro e raio , considere a região plana
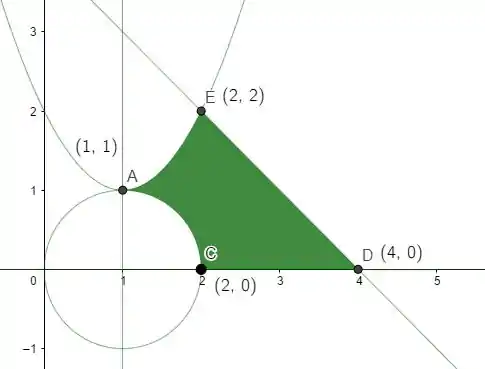
- Esboce abaixo a região . Indique explicitamente em seu desenho as coordenadas de três pontos que pertençam à fronteira da região.
- Calcule a área da região utilizando o método que preferir.
Passo 1
Caraca que região complicada! Mas vamos com calma viu? Primeiro, vamos tirar cada uma das inequações de dentro de e analisar separadamente:
Agora vamos ver as interseções entre essas regiões! Começando com as duas mais simples:
Opa, essas inequações restringem bastante! A interseção dos dois vai ficar:
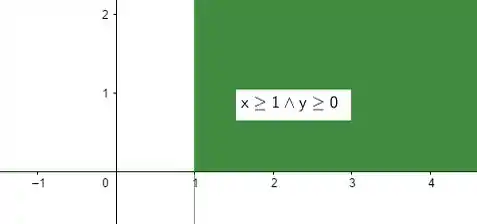
Ou seja, já sabemos que está no primeiro quadrante, mas não nele todo em! Não só não vale como temos outras restrições pra checar. Agora vamos ver essa curva:
Oras, não é que ela se parece com o enunciado? Se:
É o modelo de uma circunferência, então a curva:
É nada mais nada menos que uma circunferência de centro e raio :
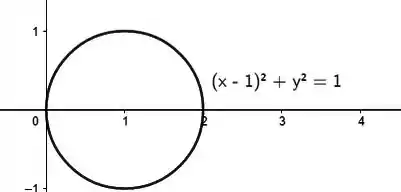
Mas como queremos:
E não:
Estamos falando então da região exterior ao círculo! A região vai ser então:
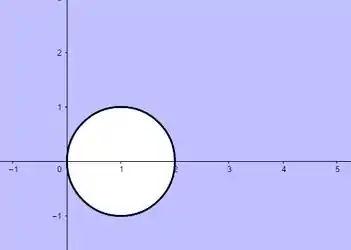
E a interseção das três regiões que vimos até agora vai ser:
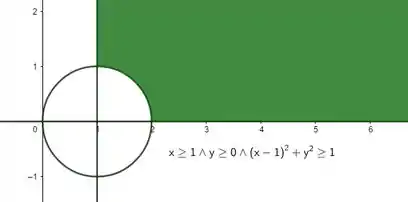
Passo 2
Beleza, já vimos de inequações. Vamos ver as outras duas:
Vamos começar com a primeira e analisar a curva:
A primeira coisa que a gente pode tentar fazer com essa malandra aí é ver suas interseções com os eixos. Partiu então. Se
Eta, então essa função não tem raíz! Afinal, não tem como qualquer número ao quadrado dar negativo! Agora, se , temos:
Então o ponto faz parte dessa curva. Agora, vamos ver um pouco sobre sua aparência: concavidade, crescimento e descrescimento! Pra isso, que tal abrir o polinômio? Saca só:
Como a primeira e a segunda derivada estão relacionadas, respectivamente, com o crescimento/decrescimento e a concavidade de uma função, a gente deriva então e fica com:
Analisando a primeira derivada, a gente vê que é uma reta! Oras, retas sempre passam alguma vez pelo eixo ! Vamos ver quando nesse caso:
Então em vamos ter um ponto crítico dessa curva. Como:

Vamos escolher dois pontos: um um pouco antes e outro um pouco depois de . Escolhendo e então, temos:
Show! Nosso ponto é então um ponto de mínimo. Quanto a concavidade, dá uma olhada na segunda derivada:
E não é que ela é constante? E positiva? Sendo assim, a concavidade vai ser sempre pra cima! Temos tudo pra esboçar o gráfico da curva agora! Bora lá:
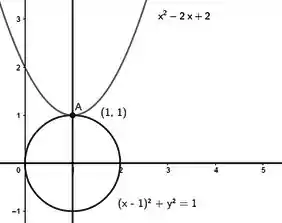
E olha só! A circunferência e a curva se encontram no ponto ! Agora que falamos da curva, vamos falar da região:
Como o símbolo é de , queremos a região abaixo da curva, beleza? Então vamos ter:
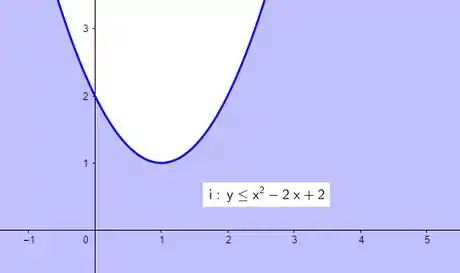
E a interseção de tudo que temos até agora fica:
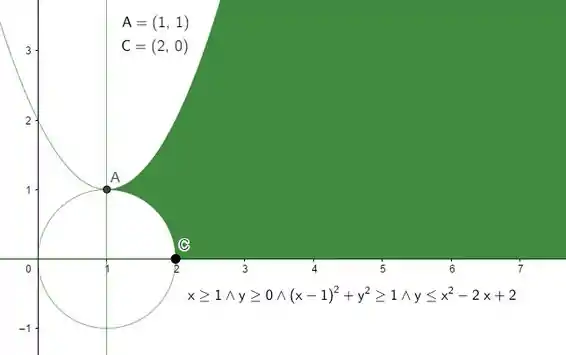
Passo 3
Bora fechar o esboço então com a última região:
Que veja bem: é uma reta! Esboçar retas é mais tranquilo! Como tem um multiplicando o , a inclinação da reta é negativa! E as interseções com os eixos, vão ser:
O esboço da reta vai ficar:
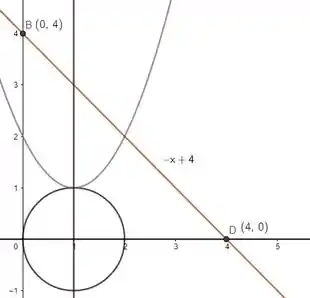
Opa, outra interseção em! Dessa vez da reta com o polinômio, ao invés do polinômio com a circunferência! Pra gente saber em que ponto essas curvas se cruzam, basta a gente igualar de cada uma, combinado? Vamos lá então:
Igualando:
E olhaí, outro polinômio de segundo grau! E sendo igualado à ? Isso cheira à Bháskara. Seja:
Onde são raízes do polinômio, usamos a fórmula de Bháskara para achar:
Portanto:
Como não estamos prestando atenção em valores negativos de , então o ponto de interseção ocorre em ! E veja bem, se:
E , então o ponto de interseção vai ser:
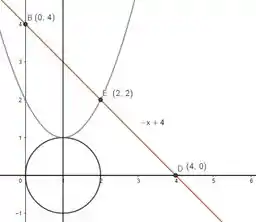
Só que aqui temos de novo uma região né, então vamos ver o sinal depois de : um sinal de menor ou igual! O que queremos então é a parte de baixo da reta, o esboço dessa região vai ser:
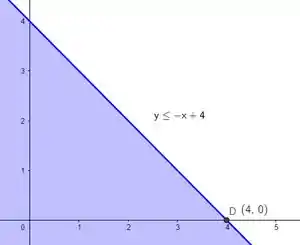
E fazendo a interseção dessa região também com todo o resto até agora, fechamos a região ! Saca só como ela fica:
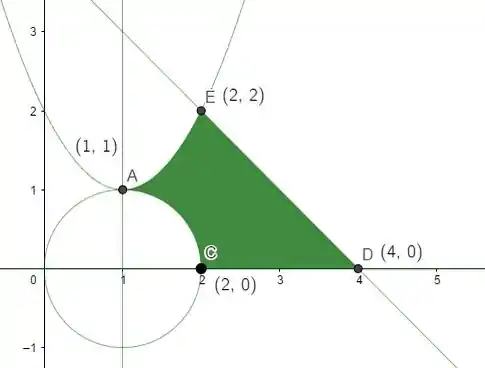
Passo 4
Pra gente fechar a questão e partir pro abraço, bora calcular a área de . Como somos livres pra calcular da forma que quisermos, vamos ser práticos, beleza? Pra começar, vamos dividir a região em duas:
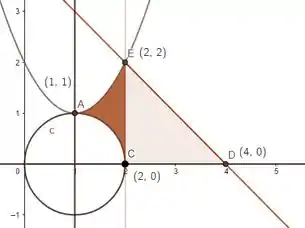
E veja só! A área marrom clara é a área de um triângulo. Sendo assim, calculamos:
Agora a área marrom escura o papo é outro: vamos precisar integrar! Mas veja bem, a área marrom pode ser entendida como a área roxa menos a área preta:
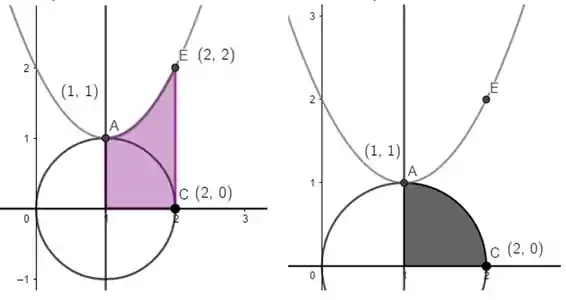
Então integrar mesmo a gente só vai precisar na área roxa! Até porque, a área preta é da área de um círculo! Bora calcular então:
Pra área roxa, temos:
E pra área preta, temos:
A área marrom escura vai ficar então:
A área total: