PF de Cálculo 1 da UFRJ - 2018.1

4a) Calcule as seguintes integrais:

4b) Calcule as seguintes integrais:

2) Considere as funções e . Prove que os gráficos de e se intersectam em um único ponto quando .

1) Seja a função definida pela expressão:

Onde é um número positivo.

1. Determine as assíntotas horizontais do gráfico de , caso elas existam
2. Determine os valores de que tornam contínua no ponto

5) Seja a região localizada no primeiro quadrante do plano cartesiano, cujos pontos estão localizados acima da reta , abaixo da parábola e abaixo da hipérbole .

1. Esboce , indicando os pontos de interseção das curvas
2. Calcule a área de

3) Na figura, as semirretas e são paralelas e o segmento é perpendicular a essas semirretas. O ponto , situado no segmento , é tal que: e . Considere a coleção de todos os triângulos retângulos , com ângulo reto em , tais que está sobre a semirreta e está sobre a semirreta .

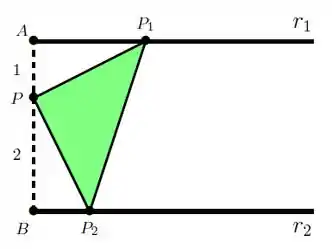
Determine a menor área possível para um triângulo dessa coleção: