3) Na figura, as semirretas e são paralelas e o segmento é perpendicular a essas semirretas. O ponto , situado no segmento , é tal que: e . Considere a coleção de todos os triângulos retângulos , com ângulo reto em , tais que está sobre a semirreta e está sobre a semirreta .
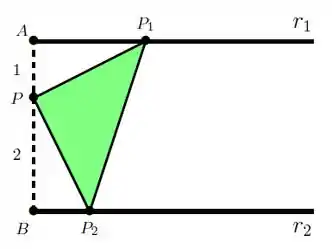
Determine a menor área possível para um triângulo dessa coleção:
Passo 1
Antes de começarmos essa questão, vamos traduzir pra desenhês o que esse enunciado quis dizer. Mantendo paradinho onde ele tá, vamos mover e de forma a criar novos triângulos retângulos. Olha um exemplo de movimento desses pontos:
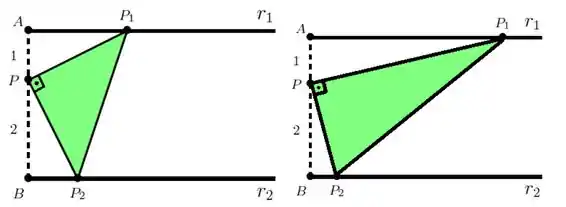
Agora que entendemos melhor o que acontece, vamos começar a relacionar variáveis, ok?
Passo 2
Vamos dar nome aos bois primeiro:
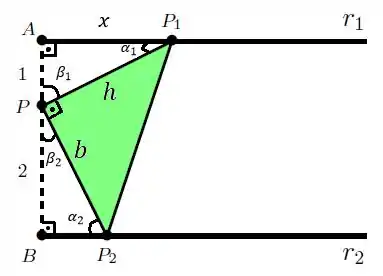
Como a área do triângulo verde é dada por:
Vamos tentar relacionar variáveis pra obter como função de uma variável só. Pra começo de conversa, vamos chamar:
Sendo o triângulo retângulo, pelo teorema de Pitágoras:
Então olha só! Já achamos uma expressão pra . Fazendo a raiz dos dois lados, temos:
Vamos tentar então achar uma expressão em função de para , que aí sim podemos escrever e finalizar a função que otimizaremos: a área. Pra isso, dá uma olhada nessas relações entre os ângulos marcados:
Passando pro outro lado:
Fazendo , temos:
E fazendo , temos:
Ou seja, do resultado e podemos ver que os triângulos e são semelhantes! E por semelhança de triângulos, podemos fazer:
O que vai dar:
E do teorema de Pitágoras para o triângulo , temos:
Show de bola, fechamos então a expressão de , vamos ter:
E agora terminamos de modelar a expressão da área! Juntando tudo que achamos temos:
O que, simplificando, fica:
Passo 3
Agora que temos , precisamos otimizar. Como queremos a menor área, temos que achar um ponto de mínimo. Oras, é só derivar e igualar à então pra gente buscar os pontos críticos dessa função! Vamos ter:
E igualando à , temos:
Como e como não existe segmentos de reta de tamanho negativo, o único ponto crítico de vai ser:
Mas será que esse ponto é de mínimo mesmo? Bem, pra gente saber, tem duas formas: a com contas e a argumentativa. Pra poupar trabalho, podemos ver que, para os limites:
A área tende ao infinito por que hora e hora tenderão ao infinito nesses limites, e logo, também irá . Podemos ver isso nessas duas figuras:
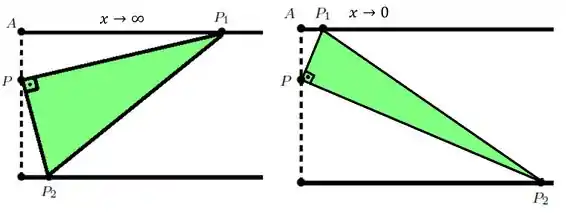
Passo 4
Agora que achamos o ponto de mínimo, basta substituir seu valor na fórmula da área! Vamos ter: