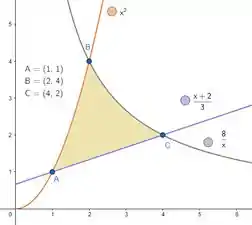
5) Seja a região localizada no primeiro quadrante do plano cartesiano, cujos pontos estão localizados acima da reta , abaixo da parábola e abaixo da hipérbole .
- Esboce , indicando os pontos de interseção das curvas
- Calcule a área de
Passo 1
Vambora então. Como a questão pede pra gente marcar no esboço os pontos de interseção que definem , vamos começar por eles. Vamos de em então, mas antes, vamos ajeitar a equação da curva:
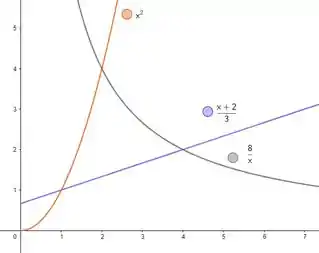
Vamos ter então três curvas pra levar em consideração, sendo elas:
Igualando e , temos:
Fazendo Bháskara, temos que:
Resolvendo, temos:
E logo:
Como estamos falando de pontos do primeiro quadrante, vamos esquecer do negativo, ok? Usando em , encontramos já o primeiro ponto:
Agora vamos igualar e . Vamos ter:
Mais rápido de achar esse ponto em! Usando em , encontramos o segundo ponto de interseção!
E agora, pra última combinação, igualamos e e ficamos com:
Mesma ideia. Usando Bháskara, chegamos à:
Ignorando de novo o valor negativo, vamos pegar só a raíz positiva, beleza? Vamos ter então:
E usando em , pegamos nosso terceiro e último ponto, que será:
Passo 2
Achamos os três pontos em que as curvas vão se encontrar. São eles:
Como é uma parábola, logo, graficamente, é algo parecido com um copo de boca pra cima, é uma reta e uma hipérbole, algo, graficamente, semelhante a uma rampa de skate, podemos esboçar as 3 curvas da seguinte forma:
E marcando os pontos de interseção e hachurando a região , vamos ter:
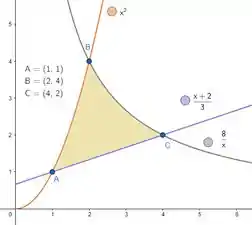
Então é só calcular a área bege para fechar a letra e partir pro abraço. Pra fazer isso, veja bem: traçando retas , e , podemos entender a área bege como a soma das áreas cinza e salmão:
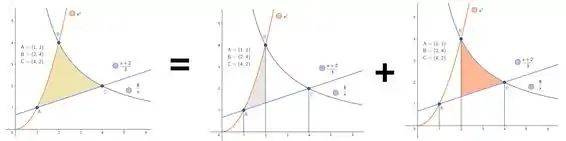
Vamos calcular em passos diferentes então a área cinza e a área salmão
Passo 3
Vamos começar pela área cinza. Pra calcular essa área, vamos também entender ela como uma operação de áreas. Saca só, podemos entender a área cinza como a área azul menos a área amarela:
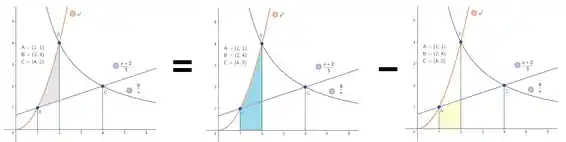
E as áreas azul e amarela sabemos calcular! Afinal, são áreas abaixo de curvas. Como a área azul é a área abaixo da curva entre e , vamos ter:
E como a área amarela é a área da reta no mesmo intervalo de , vamos ter:
A área da região cinza vai ser então
Passo 4
Agora pra área salmão, vamos dividir do mesmo jeito do passo anterior, só, claro, escolhendo cores diferentes. Podemos enxergar a área salmão como a área verde menos a área rosa:
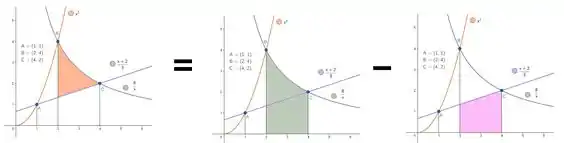
E a área dessas novas duas cores também sabemos calcular em! São integrais abaixo das suas respectivas curvas, mudando agora o intervalo de para . Sendo assim, pra área verde, como estamos falando da curva , vamos ter:
E pra área rosa, voltamos à reta, agora mudando os limites de integração. Vamos ficar com:
A área salmão então vai ser:
Passo 5
Agora bora fechar em! Como:
E já sabemos tanto a área cinza quanto a salmão, é só somar:
E logo: