P2 de Cálculo 1 da USP - 2018

ME03) Seja uma função contínua no intervalo e derivável em , que assume os valores , , e . Considere as afirmações:

1. A equação tem pelo menos uma solução no intervalo
2. A equação tem exatamente uma solução no intervalo
3. A função admite um ponto crítico no intervalo

Pode-se dizer com certeza que:

1. Todas as afirmações são falsas
2. Somente as afirmações e são verdadeiras
3. Somente as afirmações e são verdadeiras
4. Todas as afirmações são verdadeiras
5. Somente a afirmação é verdadeira

ME04) Deseja-se estimar o valor de com erro inferior a . Use um polinômio de Taylor da função em torno de e seu resto de Lagrange. Sabendo que , assinale a alternativa correspondente ao menor grau de um tal polinômio que se pode garantir com esses elementos.

ME01) Sejam dada por e cuja existência é garantida pelo Teorema do Valor Médio para no intervalo . O valor de é:

ME02) Seja dada por então:

1. e é estritamente crescente
2. Nenhuma das alternativas é correta
3. e tem um ponto de mínimo local
4. e tem um ponto de mínimo local
5. e é estritamente crescente

ME05) Seja , definida em toda reta real. O número de soluções da equação no intervalo é:

1) Seja dada por

Esboce o gráfico de localizando intervalos de crescimento e decrescimento, concavidades, limites convenientes e assíntotas (quando existirem). Use que:

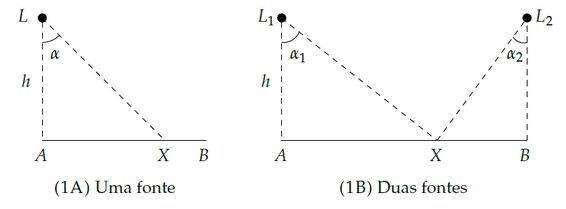
2) Sejam uma fonte luminosa puntiforme de potência e um segmento de reta que dista de (vide Figura ). A intensidade luminosa em , que dista de , é dado por:

Onde é uma constante. Considere agora, conforme a Figura , duas fontes e (com potências e e respectivamente) emitindo luz sobre os pontos de um segmento de comprimento . Mostre que existe um único ponto em sobre o qual a intensidade luminosa é máxima.