P2 de Cálculo 1 da USP - 2019
Cálculo 1 - USP
Assinale a alternativa cuja afirmação é verdadeira
- Se é uma função derivável tal que não possui pontos críticos, então não possui extremos globais
- Se é uma função qualquer tal que , então existe tal que
- Se é uma função contínua tal que é derivável em e , então existe tal que
- Se é uma função derivável e é o único ponto crítico de , então é extremo global de .
- Se é uma função derivável tal que e para todo , então para todo
Considere os cones circulares retos inscritos numa esfera de raio cujas alturas variam no intervalo . Entre esses cones, sejam o de maior volume e o de menor volume. Então a razão entre o volume de e o volume de é
Considere os cones circulares retos inscritos numa esfera de raio cujas alturas variam no intervalo . Entre esses cones, sejam o de maior volume e o de menor volume. Então a razão entre o volume de e o volume de é
Assinale a alternativa cuja afirmação é verdadeira
- Se é uma função derivável, com derivada contínua, tal que possui pontos críticos, então possui extremos locais.
- Se é uma função qualquer tal que , então existe tal que
- Se é uma função derivável, com derivada contínua, é o único ponto crítico de e é o ponto de mínimo local de então é o ponto de mínimo global de .
- Se é uma função contínua tal que é derivável em e , então existe tal que
- Se é uma função derivável tal que e para todo , então para todo
Considere a função dada por:
É correto afirmar que tem concavidade pra baixo em:
Considere a função dada por:
É correto afirmar que:
- A assíntota de quando intercepta o eixo no ponto
- A assíntota de quando intercepta o eixo no ponto
- não tem assíntota quando
- A assíntota de quando intercepta o eixo no ponto
- A assíntota de quando intercepta o eixo no ponto
Considere os cones circulares retos inscritos numa esfera de raio cujas alturas variam no intervalo . Entre esses cones, sejam o de menor volume e o de maior volume. Então a razão entre o volume de e o volume de é
Considere os cones circulares retos inscritos numa esfera de raio cujas alturas variam no intervalo . Entre esses cones, sejam o de menor volume e o de maior volume. Então a razão entre o volume de e o volume de é
Considere a função dada por:
É correto afirmar que é estritamente decrescente em:
Considere a função dada por:
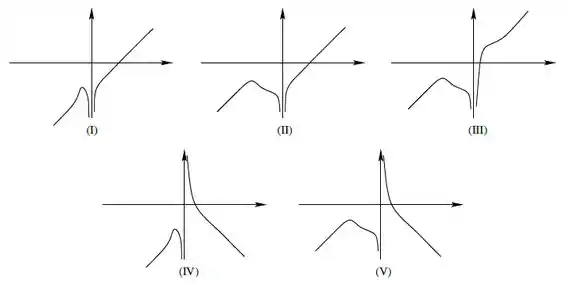
Assinale a alternativa cujo gráfico mais se assemelha ao gráfico de :
Considere a função dada por:
Assinale a alternativa cujo gráfico mais se assemelha ao gráfico de :
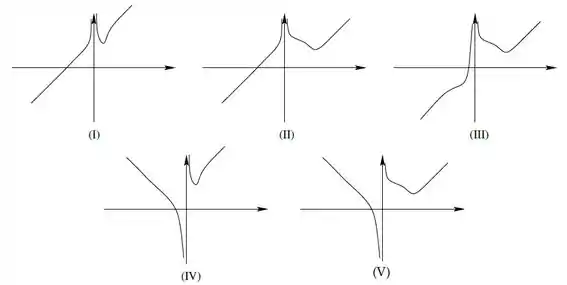
Considere a função dada por:
É correto afirmar que tem concavidade pra cima em:
Considere a função dada por:
É correto afirmar que é estritamente decrescente em:
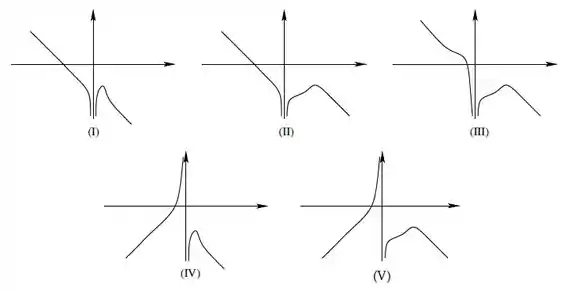
Considere a função dada por:
Assinale a alternativa cujo gráfico mais se assemelha ao gráfico de :
Considere a função dada por:
É correto afirmar que:
- A assíntota de quando intercepta o eixo no ponto
- A assíntota de quando intercepta o eixo no ponto
- não tem assíntota quando
- A assíntota de quando intercepta o eixo no ponto
- A assíntota de quando intercepta o eixo no ponto
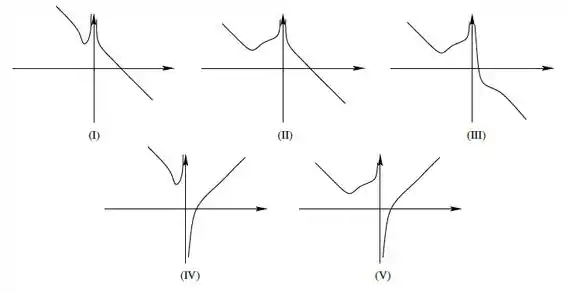
Considere a função dada por:
É correto afirmar que tem concavidade pra baixo em:
Considere a função dada por:
É correto afirmar que:
- A assíntota de quando intercepta o eixo no ponto
- A assíntota de quando intercepta o eixo no ponto
- não tem assíntota quando
- A assíntota de quando intercepta o eixo no ponto
- A assíntota de quando intercepta o eixo no ponto
Considere a função dada por:
É correto afirmar que é estritamente crescente em:
Considere a função dada por:
É correto afirmar que tem concavidade pra cima em:
Considere a função dada por:
É correto afirmar que é estritamente crescente em:
Seja uma função derivável tal que:
- e ;
- As retas e são assíntotas para ;
- tem exatamente raízes, e o gráfico de no intervalo está esboçado na figura abaixo
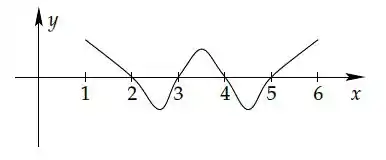
É correto dizer que o número de raízes de no intervalo é
Seja uma função derivável tal que:
- ;
- As retas e são assíntotas para ;
- tem exatamente raízes, e o gráfico de no intervalo está esboçado na figura abaixo
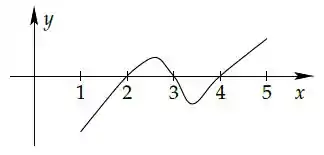
É correto dizer que o número de raízes de no intervalo é
Seja uma função derivável tal que:
- ;
- As retas e são assíntotas para ;
- tem exatamente raízes, e o gráfico de no intervalo está esboçado na figura abaixo
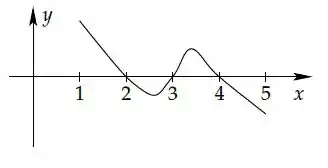
É correto dizer que o número de raízes de no intervalo é
Seja uma função derivável tal que:
- e ;
- As retas e são assíntotas para ;
- tem exatamente raízes, e o gráfico de no intervalo está esboçado na figura abaixo
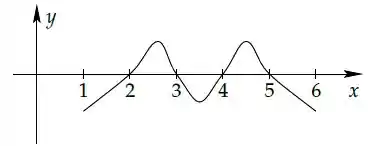
É correto dizer que o número de raízes de no intervalo é