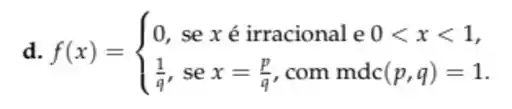Listas de Cálculo 1 - USP de Cálculo 1 da USP - Lista 1
Cálculo 1 - USP
1.2. A resolução abaixo está INCORRETA. Indique onde ocorrem os erros e então calcule o limite correta.
Ver solução completa2016) Os limites e valem, respectivamente,
a. e +; b. e −; c. e +; d. e −; e. nenhuma das anteriores;
Ver solução completaDizemos que duas funções reais f e g, são equivalentes se . Indicamos isso escrevendo f ∼ g. Qual das afirmações abaixo NÃO é consequência de f ∼ g?
a. ; b. ; c. ; d. ; e. .
Ver solução completaDecida se cada uma das afirmações abaixo é verdadeira ou falsa, justificando ou apresentando um contra-exemplo.
a. Se f , g : R → R são funções tais que f é limitada e positiva e , então tem-se que .
b. Se f , g : R → R são funções tais que f é limitada e , então tem-se que .
c. Se f , g : R → R são funções tais que , então .
Ver solução completaConsidere a afirmação “Sejam funções tais que e é limitada. Então ”. É correto dizer
- Tal afirmação é verdadeira
- Tal afirmação é verdadeira se supomos que
- Tal afirmação é verdadeira se supomos que exista algum tal que para todo
- Tal afirmação é verdadeira se supomos que exista algum tal que para todo
- Tal afirmação é falsa para toda limitada
Determine, se existir, o valor para que cada uma das funções abaixo seja contínua
Ver solução completaDetermine, se existir, o valor para que cada uma das funções abaixo sejam contínuas
Ver solução completaSeja a função dada por . Para quantos valores de o gráfico de tem reta tangente horizontal?
- Nenhum
- 1
- 2
- 3
- Infinitos
Sejam f : R → R derivável em = 0 tal que f(0) = f ′ (0) = 0 e g : R → R uma função limitada (não necessariamente derivável em x0 = 0). A função h(x) = f(x)g(x) é derivável em = 0? Exiba h ′ (0) em caso afirmativo
Ver solução completaResponda, justificando:
a. Se f + g é derivável em , é verdade que f e g são necessariamente deriváveis em ?
b. Se f · g é derivável em , quais condições sobre f garantem a derivabilidade de g em ?
Ver solução completaProve que:
a. Se f é derivável em , então | f(x)| é derivável em , desde que f() ≠0. Dê um contra-exemplo no caso em que f() = 0.
b. Não é possível escrever x = f(x)g(x) com f , g deriváveis tais que f(0) = g(0) = 0
Ver solução completaSeja f uma função derivável em e considere a função . Calcule e . Interprete geometricamente os resultados obtidos.
Ver solução completaSuponha que f é uma função derivável em = 0 e que f(0) = 0. Mostre que para alguma função g que é contínua em = 0.
Dica: O que acontece se você tentar escrever ?
Ver solução completaSejam f , g : R → R tais que:
(i) f é contínua em x = 0 e
(ii) g é descontínua em x = 0.
Pode-se concluir corretamente que é descontínua em x = 0 a função:
a. f + g; b. f g; c. f ◦ g; d. g ◦ f ; e. |g|.
Ver solução completa3.33. Seja uma função dada implicitamente pela equação . Admitindo que é derivável, determine a reta tangente ao gráfico de no ponto .
Ver solução completa3.34. Seja derivável, onde é um intervalo aberto contendo . Suponha que , para todo ∈ . Encontre e a equação da reta tangente ao gráfico de no ponto .
Ver solução completa3.35. (P1-2016) Seja uma função derivável definida em um intervalo aberto centrado em e dada implicitamente pela equação . O valor de é
a)
b)
c)
d)
e)
Ver solução completa4.1. Suponha que seja uma função injetora, derivável, e que sua inversa, , também seja derivável. Mostre que
Ver solução completaUm objeto circular tem seu raio variando de maneira desconhecida, mas sabe-se que quando seu raio e , a taxa de variação deste e . Determine a taxa de variação da área do objeto no instante em que seu raio e .
Ver solução completaSuponha agora que o objeto circular do exercício anterior e, na verdade, um equador de um objeto esférico. Determine a taxa de variação do volume do objeto e de sua área, quando o raio é .
Ver solução completaA área entre dois círculos concêntricos variáveis �� constante igual a . A taxa de variação da área do círculo maior é de . Qual a taxa de variação do raio em relação ao tempo do círculo menor quando ele tem área ?
Ver solução completaA partícula A se move ao longo do semieixo positivo e a partícula B move-se ao longo do gráfico da função . Num certo instante, a partícula A está no ponto (5, 0) e afasta-se da origem com velocidade unidades por segundo e a distância de B até a origem e unidades, afastando-se da origem com velocidade unidades por segundo. Qual a taxa de variação da distância entre A e B nesse instante?
Ver solução completaNum certo instante , a altura de um triangulo cresce a razão e sua área aumenta a razão de . No instante , sabendo que sua altura a e sua área e , qual a taxa de variação em relação ao tempo da base do triangulo?
Ver solução completaDespeja-se areia sobre o chão fazendo um monte que tem, a cada instante, a forma de um cone com diâmetro da base igual a três vezes a altura. Quando a altura do monte e de , a taxa de variação com que a areia e despejada e de . Qual a taxa de variação da altura do monte neste instante?
Ver solução completaUma lâmpada esta acesa no solo a de um edifício. Um homem de de altura anda a partir da luz em direção ao edifício a . Determine a velocidade com que o comprimento de sua sombra sobre o edifício diminui quando ele está a do edifício e quando ele está a do edifício.
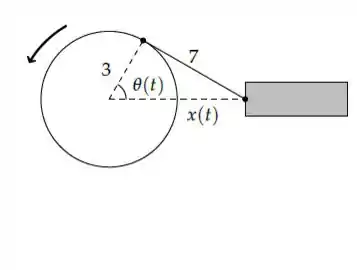
Ver solução completaNum motor a combustão, uma biela de tem uma de suas extremidades acoplada a uma manivela cujo raio é de . Na outra extremidade da biela está um pistão que se move quando a manivela gira (vide Figura abaixo). Sabendo que a manivela gira no sentido anti-horário a uma taxa constante de rotações por minuto, calcule a velocidade do pistão quando o ângulo de rotação do disco é (medido a partir da posição em que o pistão está mais afastado do disco).
Uma escada de bombeiro com está encostada na parede de um prédio e sua base se afasta da parede. Num certo instante, a base da escada se encontra a da parede e sua velocidade é de .
- Qual a velocidade com a qual o topo da escada se move nesse instante?
Uma escada de bombeiro com está encostada na parede de um prédio e sua base se afasta da parede. Num certo instante, a base da escada se encontra a da parede e sua velocidade é de .
b) Considere o triângulo formado pela parede da casa, a escada e o chão. Calcule a taxa de variação da área deste triangulo no instante em que a base da escada se encontra a da parede.
Ver solução completaUma escada de bombeiro com está encostada na parede de um prédio e sua base se afasta da parede. Num certo instante, a base da escada se encontra a da parede e sua velocidade é de .
c) Calcule a taxa de variação do ângulo formado entre a parede da casa e a escada, quando a base da escada estiver a da parede.
Ver solução completaSeja f : R → R a função dada por f(x) = { , se ∈ Q; , se ∈ R \ Q.
O conjunto descontinuidades de f é: a. ∅; b. Q; c. R \ Q; d. R \ {0}; e. R.
Ver solução completaPara que a função , se ; , se . seja contínua em R o valor da constante k deve ser:
a. −7; b. 1; c. 3; d. −1; e. −5.
Ver solução completaSejam e funções deriváveis em um intervalo aberto e
Mostre que é derivável em se e somente se e . Construa contraexemplos removendo uma das condições de cada vez
Ver solução completaVerifique se cada uma das funções abaixo é contínua e se é derivável no ponto indicado.
Ver solução completaVerifique se cada uma das funções abaixo é contínua e se é derivável no ponto indicado.
Ver solução completaVerifique se cada uma das funções abaixo é contínua e se é derivável no ponto indicado.
Ver solução completaVerifique se cada uma das funções abaixo é contínua e se é derivável no ponto indicado.
Ver solução completaSeja uma função real tal que para todo . Então
a. pode ser descontínua em ;
b. é contínua em , mas pode não ser derivável em ;
c. é derivável em e ;
d. é derivável em e ;
e. é derivável em mas podemos apenas afirmar que .
Ver solução completaConsidere a função f(x) = x|x|. Decida se f é derivável em e calcule f′(0) em caso afirmativo.
Ver solução completa7.17. Use o TVM para provar as seguintes desigualdades:
(b) , para todos , com e .
Ver solução completa7.17. Use o TVM para provar as seguintes desigualdades:
(c) , para todos , com e .
Ver solução completa7.17. Use o TVM para provar as seguintes desigualdades:
(d) , para todos , com .
Ver solução completa7.17. Use o TVM para provar as seguintes desigualdades:
(e) , para todos , com .
Ver solução completa7.18. Seja uma função derivável no intervalo tal que e , para todo . Mostre que , para todos .
Ver solução completaLatas cilíndricas fechadas devem ser feitas com um volume especificado. Qual é a razão entre a altura e o diâmetro da base que minimiza a quantidade de metal gasto para fazer a lata?
Por que as latas encontradas no mercado não são, em geral, como em Tipicamente, o metal é entregue em chapas retangulares. Não há desperdício envolvido em cortar a chapa que formará a superfície lateral, mas as tampas devem ser cortadas de uma peça quadrada e as sobreas são recicladas. Ache a razão entre a altura e o diâmetro de uma lata de volume que minimiza o custo do material utilizado.
Ver solução completaDetermine o cone circular reto de maior volume que pode ser inscrito numa esfera de raio .
Ver solução completaSejam o círculo de raio e centro em e , o círculo de raio , , e centro em . Sejam ainda o ponto e o ponto de intersecção dos círculos e situado no primeiro quadrante.
Se é a intersecção da reta com o eixo , o que acontecerá com , quando encolher arbitrariamente?
Ver solução completaDecida se a afirmação é verdadeira ou falsa, justificando ou apresentando um contra-exemplo.
a. Se f : R → R é tal que | f | é contínua em x = 0, então f é contínua em x = 0.
b. Se f e g são funções descontínuas em x = 0, então a função f g é descontínua em x = 0.
Ver solução completaSeja f : R → R tal que e existe k ∈ R de modo que para todos e temos
Então é igual a: a. 1/6; b. 1/3; c. 1/2; d. 2/3; e. 5/6.
Ver solução completaSeja , se ; 0, se .
Em pode-se afirmar que f é
a. descontínua;
b. derivável e ;
c. contínua mas não derivável;
d. derivável e ;
e. derivável e .
Ver solução completaDizemos que é uma raiz dupla de uma função polinomial f se , para alguma outra função polinomial .
a. Mostre que é raiz dupla de f se e somente se é raiz tanto de f quanto de f ′.
b. Quando tem raiz dupla? Interprete geometricamente.
Ver solução completaUm ponto desloca-se sobre o gráfico da curva . No instante em que ele se encontra no ponto (2,), a taxa de variação de sua abscissa é 10m/s. A taxa de variação da distância do ponto até a origem neste mesmo instante é
a. ; b. ; c. ; d. ; e. −.
Ver solução completaDeseja-se construir uma esfera e um cubo de modo que a soma das áreas de suas superfícies seja igual a . Determine o raio da esfera que maximiza e o que minimiza a soma de seus volumes.
Ver solução completaUm cilindro é obtido girando-se um retângulo ao redor do eixo , onde a base do retângulo está apoiada. Seus vértices superiores estão sobre a curva Qual é o maior volume que tal cilindro pode ter?
Ver solução completaDentre os cilindros circulares inscritos numa esfera de raio , seja a altura daquele que tem volume máximo e seja a altura daquele que tem superfície lateral máxima. Então, é:
Ver solução completaSejam e duas retas paralelas com a distância entre eles igual a . Fixe um ponto sobre a reta . Fixe dois pontos e sobre a reta de modo que a distância entre os pontos e seja igual a . É possível encontrar um ponto na reta , de modo que o segmento intercepte o segmento em um ponto de forma que a soma das áreas dos triângulos e seja mínima? E seja máxima? Nos casos em que a resposta for afirmativa, determine a altura do triângulo
Ver solução completaSejam . Determine, caso exista, o perímetro mínimo dos triângulos de base e altura (relativa à base dada) .
Ver solução completaConsidere todos os triângulos retângulos formados pelos semieixos positivos e por uma reta que passa pelo ponto . Dentre todos esses triângulos, aquele que possui área mínima tem a hipotenusa valendo:
Ver solução completaUm arame de comprimento deve ser cortado em pedaços, um para formar um quadrado e outro um triângulo equilátero. Como se deve cortar o arame para que a soma das áreas cercadas pelos pedaços seja:
máxima?
mínima?
Mostre que no caso o lado do quadrado é da altura do triângulo.
Ver solução completaUm muro de metros de altura está a metro de distância da parede lateral de um prédio. Qual o comprimento da menor escada cujas extremidades se apoiam uma na parede, e outra no chão do lado de fora do muro?
Ver solução completaSejam um intervalo aberto e uma função derivável. Assuma que vale o seguinte teorema: se , com , então para todo entre e , existe tal que . (Observe que não supomos de classe . Com base nesse teorema podemos afirmar que:
Não existe função , derivável, tal que e para todo .
toda função derivável em possui sua derivada contínua em .
toda função derivável em possui descontínua em todo ponto de .
nenhuma das alternativas anteriores é correta.
Ver solução completaSeja derivável e com um único ponto crítico . Prove que se for ponto de mínimo (máximo) local de , então será o único ponto de mínimo(máximo) global de .
Ver solução completaDentre todas as retas tangentes ao gráfico de , a única que passa pelo ponto é:
- ;
- ;
- ;
- ;
Considere todas as retas que são simultaneamente tangentes às parábolas e . Então o produto dos coeficientes angulares dessas retas é:
Sejam cujos gráficos são:
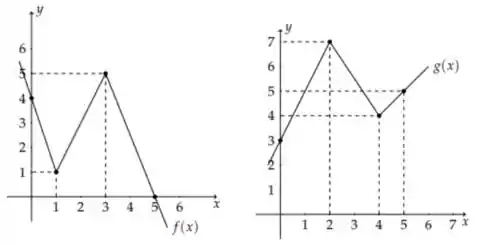
Sejam dadas por e . O valor é:
a) ;
b) ;
c) ;
d) ;
e) .
Ver solução completaSejam cujos gráficos são:
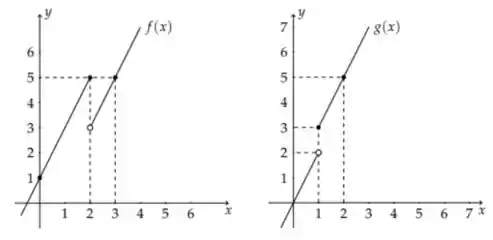
Então pode-se dizer que :
a) não é derivável somente em ;
b) não é derivável somente em ;
c) não é derivável somente em e ;
d) é derivável em todos os pontos e ;
e) é derivável em todos os pontos e .
Ver solução completaDecida, justificando ou apresentando contra-exemplo, se cada uma das sentenças abaixo é verdadeira ou falsa:
a. Se f é derivável em , então | f(x)| é derivável em , desde que f() ≠0. E no caso em que f() = 0?
b. Se f, g são duas funções deriváveis em , então as funções e são deriváveis em ;
c. Suponha , onde g é uma função contínua em = 0. Então f é derivável em = 0. Se for verdadeira, calcule f ′ (0) em termos de g;
d. É possível escrever x = f(x)g(x) com f , g deriváveis tais que f(0) = g(0) = 0.
Ver solução completaConsidere as seguintes afirmações:
Se é limitada e , então .
Se é uma função tal que então, é derivável.
Se é descontínua em e limitada então, é derivável em .
São corretas
a. nenhuma das afirmações;
b. todas as afirmações;
c. somente as afirmações e ;
d. somente as afirmações e ;
e. somente as afirmações e .
Ver solução completaDetermine todos os pontos sobre a curva tais que a reta tangente à curva em seja paralela à reta .
Ver solução completaMostre que qualquer par de retas tangentes à parábola , () tem como interseção um ponto que está numa reta vertical que passa pelo ponto médio do segmento que une os pontos de tangência destas retas.
Ver solução completaSuponha que é contínua, e é um número racional para todo o . Prove que , para todo .
Ver solução completaSeja uma função contínua no intervalo e derivável em , que assume os valores
Considere as afirmações:
A equação tem pelo menos uma solução no intervalo .
A equação tem exatamente uma solução no intervalo .
A função admite um ponto crítico no intervalo .
Pode-se dizer com certeza que:
a. todas as afirmações são falsa.
b. somente as afirmações e são verdadeiras.
c. somente as afirmações e são verdadeiras.
d. todas as afirmações são verdadeiras.
e. somente a afirmação é verdadeira.
Ver solução completa7.27. (Transferência Fuvest 2012) Seja . Então, o coeficiente angular máximo das retas tangentes ao gráfico de é
a. ;
b. ;
c. ;
d. ;
e. .
Ver solução completa7.23. Determine, caso exista, a constante a para que tenha
a. um ponto de mínimo local em .
Ver solução completa7.23. Determine, caso exista, a constante a para que tenha
b. um ponto de mínimo local em .
Mostre ainda que, para qualquer valor de , a função não terá um ponto de máximo local.
Ver solução completa7.12. Seja . Quantas soluções distintas tem a equação ? Mostre que a equação tem exatamente três soluções reais distintas.
Ver solução completa7.26. (P2, 2016) Seja definida no intervalo fechado . Se é o valor máximo de e se é o valor mínimo de , então o produto é
a. ;
b. ;
c. ;
d. ;
e. .
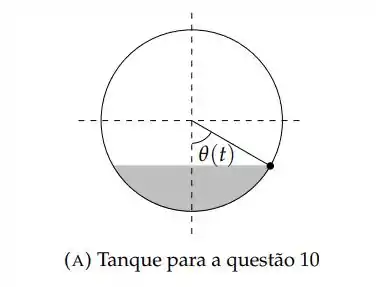
Ver solução completaUma mangueira está enchendo um tanque de gasolina que tem o formato de um cilindro “deitado” de diâmetro 2m e comprimento 3m. A figura 2a representa uma seção transversal do tanque no instante t. O ângulo θ varia de zero (tanque vazio) a π (tanque cheio). No instante em que a altura h do líquido é de 0.5m, a vazão é de 0.9m3/min. Determine a taxa de variação do ângulo θ nesse instante. Determine também a taxa de variação da altura h do neste mesmo instante.
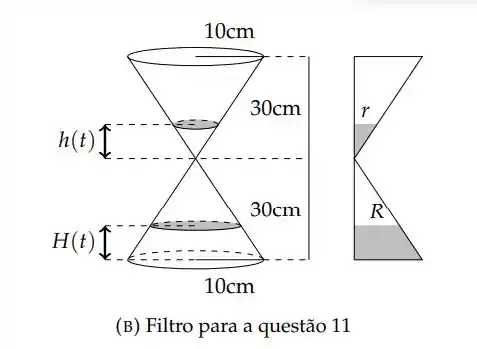
Num filtro com formato de cone, como na figura 3a, um líquido escoa da parte superior para a parte inferior passando por um orifício de dimensões desprezíveis. Num certo instante, a altura H do líquido depositado na parte inferior é 8 cm, a altura h do líquido da parte superior é 10 cm e h está diminuindo a uma taxa de variação instantânea de 2 cm/min. Calcule a taxa de variação de H em relação ao tempo nesse instante.
Sejam derivável e tais que . Determine qual das
alternativas abaixo implica a existência de um c entre tal que
Ver solução completaDentre as alternativas abaixo, aquela que contém um polinômio que define uma função
bijetora de R em R é:
Ver solução completaSeja derivável em e seja dada por , . Suponha que é ponto crítico
de . Prove que
Prove que a reta tangente ao gráfico de f no ponto de
abscissa passa pela origem.
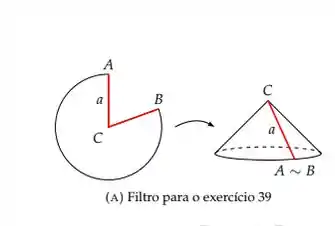
Ver solução completaUm papel de filtro circular de raio a deve ser transformado em um filtro cônico cortando um
setor circular e juntando as arestas CA e CB (veja a Figura 3a). Ache a razão entre o raio e a
profundidade do filtro de capacidade máxima.
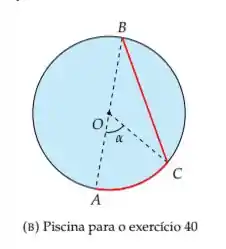
Para ir de um ponto a um ponto diametralmente oposto de uma piscina circular de de diâmetro, uma pessoa pode caminhar (com velocidade constante) pela borda da piscina até um ponto e nadar (com velocidade constante) em linha reta até o ponto (vide Figura 3b). Seja o ângulo . Sabendo que ela pode caminhar duas vezes mais rápido do que pode nadar, determine, em termos de , as trajetórias que o levam ao seu destino no maior e no menor tempo. (Observação: considere que a pessoa pode somente caminhar ou somente nadar).