ME05) Seja , definida em toda reta real. O número de soluções da equação no intervalo é:
Passo 1
Uma boa forma de se resolver essa questão é a gente tentar desenhar um pouquinho. Calma, juro que é só um pouco. Veja bem, o intervalo é né, então vamos ver os pontos extremos desse intervalo. Pra isso, como:
Pra facilitar nosso esboço, vamos considerar essa valor. Vamos ter que:
Bora então marcar os pontos:
E a reta:
Num gráfico:
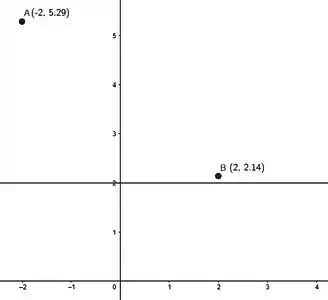
Quando a função pergunta pra gente quantas soluções possui, sabendo que a função é contínua, é a mesma coisa que perguntar quantas vezes a curva da função corta a reta horizontal saindo de A e indo até B. Algumas coisas que poderiam acontecer:
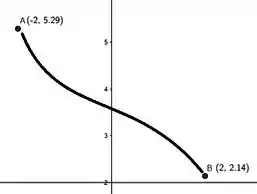
Nesse caso, a função seria estritamente decrescente e não teria solução
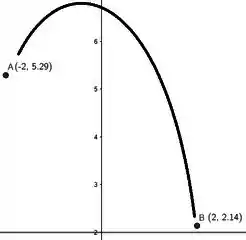
Nesse caso, a função teria um ponto de máximo só e não teria solução
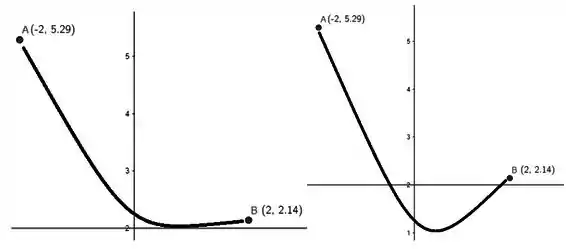
Já nesse, a função teria um ponto de mínimo só e teria uma ou duas soluções. Mas bem, isso foram só alguns exemplos pra mostrar uma coisa importante: vamos precisar saber da inclinação da reta tangente no intervalo pra responder a questão. Então bora achar:
Passo 2
Como inclinação da reta tangente tem tudo a ver com a primeira derivada, vamos derivar então:
Vimos no passo 1 quer uma das formas de ter solução é ter ponto de mínimo. Como ponto de mínimo é um ponto crítico, pra achar todos os pontos críticos de basta fazer:
Vamos ter então:
Opa, olha só! Então temos sim um ponto crítico! E ainda melhor, ele está dentro do intervalo . Vamos ver que tipo de ponto crítico é ele analisando o sinal da derivada antes e depois de . Pra , por exemplo, vamos ter:
E para , vamos ter:
Beleza, antes a função decrescia porque a primeira derivada é negativa. Chegou em passou a crescer, já que a primeira derivada passa a ser positiva. Temos então que:
Passo 3
Pelo menos uma solução então vai ter. Pra saber se vai ser uma solução só ou não, temos que verificar se
Se sim, vamos ter uma solução. Agora, se:
Vamos ter duas soluções. E ainda, se:
Ficamos sem solução nenhuma. Partiu calcular então:
E como , fechamos a questão: vão ser duas soluções!