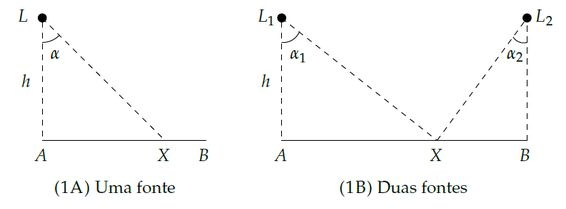
2) Sejam uma fonte luminosa puntiforme de potência e um segmento de reta que dista de (vide Figura ). A intensidade luminosa em , que dista de , é dado por:
Onde é uma constante. Considere agora, conforme a Figura , duas fontes e (com potências e e respectivamente) emitindo luz sobre os pontos de um segmento de comprimento . Mostre que existe um único ponto em sobre o qual a intensidade luminosa é máxima.
Passo 1
Eta enunciado enrolado sô! Mas vamos com calma que dá tudo certo. Pra começar, vamos notar o seguinte: se a intensidade luminosa sobre o ponto sobre para uma fonte é:
Então para duas fontes luminosas vai ser:
Se olharmos bem a figura, vemos que cada uma das duas fontes tem seu próprio ângulo, sua própria potência e sua própria distância do ponto (expresso por , representando a hipotenusa dos triângulos retângulos). Sendo assim, ficamos com:
E agora, veja bem: A intensidade vai ser escrita em função de ! O próprio enunciado dá essa ajuda pra gente. Infelizmente, não tem moleza nenhuma: vamos ter que relacionar as variáveis. Então vamos começar.
Passo 2
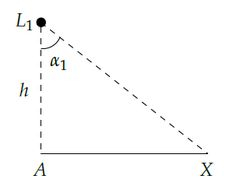
Vamos começar a falar dos ângulos representados na figura. Da figura , vemos dois triângulos retângulos que podem ser separados pra gente entender melhor. Para o triângulo da esquerda então:
E para o triângulo da direita:
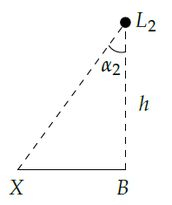
Reescrevemos então a equação da intensidade luminosa para:
Agora, ainda na figura , vemos que esses trângulos
- Alturas iguais e iguais à
- Bases diferentes
Se as bases são diferentes, vamos tentar modelar uma pra cada triângulo. Pra isso, vamos ver quem é a base dos dois juntos: a própria reta ! E dp enunciado, temos:
Então seja:
Vamos ter que, pro triângulo retângulo da esquerda, referente à , a distância é:
E pro triângulo da esquerda:
Pra encaixar essas fórmulas que vieram de Pitágoras na equação da intensidade luminosa, primeiro, elevamos os dois lados da equação por . Ficamos com:
E logo a equação da intensidade luminosa vira:
Passo 3
Veja bem, na última versão da equação da intensidade luminosa:
Tanto quanto , e são constante,s deixando realmente a intensidade agora como uma função de . Pra deixar um pouco menor essa equação, vamos chamar:
A equação se torna:
Já que a ideia é mostrar que existe uma intensidade máxima, precisamos achar o ponto de máximo de . Pra isso precisamos derivar e igualar à , beleza? Vamos ter então:
Deixando tudo no mesmo denominador, temos:
E igualando ficamos na real com:
Passo 4
Paramos então em:
Pode parecer um pouco complicado ainda, mas saca só. O valor de , como ele caminha de até , está, necessariamente, entre:
Seja
E tendo:
O que quer dizer que:
E olha só, olha lá! O Teorema do Valor Intermediário vai então nos garantir que exista pelo menos um tal que . Então de fato vai possuir um ponto crítico, já que basta para que seja verdade. Ainda não sabemos se esse ponto crítico é único no entanto. Pra saber, temos que ver se é estritamente decrescente ou não. Pra isso, derivamos:
Abrindo os termos:
Para os termos com , vamos colocar em evidência
Para os termos com , vamos colocar em evidência
Agora vamos analisar esse um tico mais simplificado. Pra isso, vamos dividir ele em 4 pedaços. O primeiro vai ser “”. Veja que no intervalo
Esse pedaço terá sempre um valor positivo. Basta substituir os extremos desse intervalo pra ver que nenhum deles tem valor negativo. O mesmo vai valer pro termo “” pelos mesmos motivos. Agora, veja bem, temos dois termos ainda pra checar:
Como ambos são polinômios de segundo grau em relação à , com sinal de negativo no termo de maior grau, o gráfico desses polinômio é como se fosse um “copo” com a boca pra baixo. Se, além disso, os polinômios não tiverem raízes, então eles serão sempre negativos. Vamos checar. Pro primeiro polinômio:
Para o segundo polinômio:
Como nos dois casos temos:
Então os dois polinômios são sempre negativos, qualquer que seja . Juntanto as informações de sinais de , chegamos à:
Opa, então está provado! Se , então é estritamente decrescente, garantindo que tem um ponto crítico único!
Passo 5
Pra fechar, falta vermos se esse ponto crítico único é realmente de máximo. Para lembrar, temos que:
E olha só! Não é que o denominador de vai ser sempre positivo no intervalo ? Sendo assim, quem vai mandar no sinal de é o sinal de . Boas notícias então meu povo, porque como provamos que é estritamente decrescente, seja tal que:
E seja:
Ficarmos com:
Se tem inclinação de reta tangente positiva antes de e inclinação degativa depois de , então de fato esse ponto crítico é um ponto de máximo!
Ufa, acabamos essa questão!
Resposta
Prova-se que possui pelo menos um ponto crítico
Prova-se ponto crítico único pelo comportamento de
Classifica-se o ponto crítico conforme o sinal de