P1 de Cálculo 2 da USP - 2010

O limite a seguir existe? Se sim, igual a quanto?

Sejam e . Esboce a imagem de e mostre que a ela está contida em uma curva de nível de , indicando qual é o nível.

O limite a seguir existe? Se sim, igual a quanto?

Sejam e , . Sabendo que a imagem de está contida no gráfico de , encontre . Esboce .

Sejam e as superfícies

a) Encontre uma parametrização para a curva dada pela interseção de e .

b) Determine a equação da reta tangente à curva do passo anterior, no ponto .

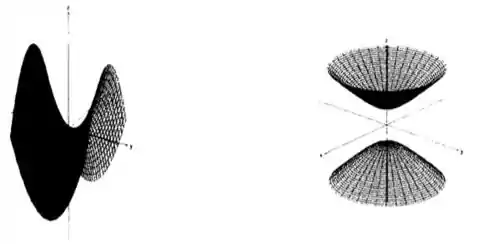
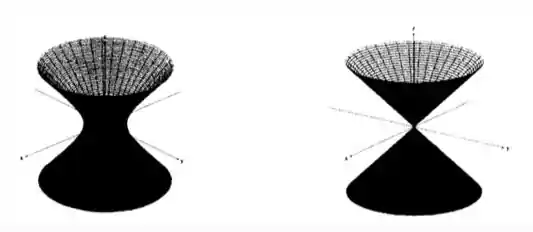
Cada uma das figuras abaixo representa uma superfície. Na coluna da tabela, temos uma equação para cada uma dessas superfícies. Cada superfície contém a imagem de uma das curvas da coluna . Escreva abaixo de cada figura qual é a curva cuja imagem está contida na superfície que ela representa:

Seja

a) Esboce as curvas de nível de nos níveis e .

b) Existe ? Justifique.