Cada uma das figuras abaixo representa uma superfície. Na coluna da tabela, temos uma equação para cada uma dessas superfícies. Cada superfície contém a imagem de uma das curvas da coluna . Escreva abaixo de cada figura qual é a curva cuja imagem está contida na superfície que ela representa:

Passo 1
Vamos lá! Primeiro, escolhemos uma superfície da coluna , e, depois, vemos qual é a curva de nível correspondente, tudo bem?
Para descobrir a superfície, basta que zeremos cada variável, uma por vez, e analisemos a curva resultante do corte feito pelo plano formado pelas outras duas variáveis.
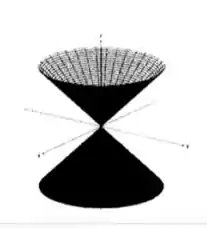
Por exemplo, para a primeira superfície:
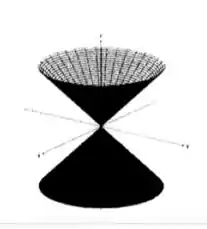
Se zeramos a variável , estamos no plano , que, quando corta a superfície nos dá:
Ou seja, um par de retas no plano !
Da mesma forma, zerando a variável , temos o mesmo par de retas, mas no plano !
E, para qualquer nível , temos:
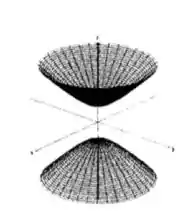
Veja que, como está ao quadrado, pode ser negativo, ou positivo, que não teremos nenhuma indeterminação! E as curvas de nível são circunferências, no caso, de raio , e paralelas ao plano . Assim, temos que corresponde ao duplo cone:
Passo 2
E qual é a curva de nível que atende a equação desse cone? Basta vermos uma que a primeira coordenada ao quadrado somada com a segunda ao quadrado dê a terceira ao quadrado, pois a equação da superfície é !
A única curva que atende a esse requisito é a , pois
Show, já matamos uma!
Passo 3
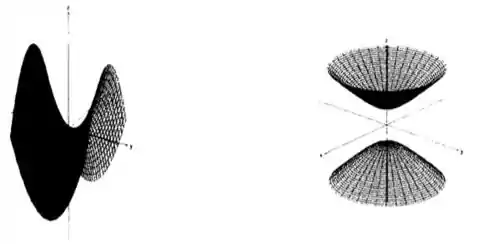
Partindo para a próxima, temos a seguinte superfície:
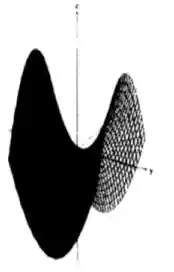
Pelo mesmo processo, se tornarmos a variável , estamos andando pelo plano , certo? E teremos a curva:
Que é a clássica parábola! Neste caso, lembre, ela está no plano , e aponta no sentido do eixo , pois o coeficiente de é , que é maior que ;)
Zerando, agora, o , teremos:
Que é uma outra parábola, né? Mas, dessa vez, está com a boa para baixo, apontando no sentido negativo do eixo !
Prosseguindo, se zeramos , temos:
Ou seja, no plano , em , temos um par de retas, simétricas, que passam pela origem! Essas retas, percebam, são seriam “retas” se ! Veja, colocando , temos:
Que é uma hipérbole! Já pegou a ideia? Temos parábolas e hipérboles... estamos num paraboloide hiperbólico!
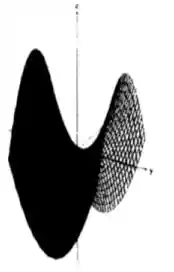
Perfeito, já matamos outra superfície!
Passo 4
E agora? Para encontrar a curva de nível que corresponde ao nosso paraboloide hiperbólico, temos que ver qual delas atende ao requisito: a segunda coordenada ao quadrado menos a primeira coordenada ao quadrado deve ser igual a terceira coordenada:
A única curva que isso acontece é a
Passo 5
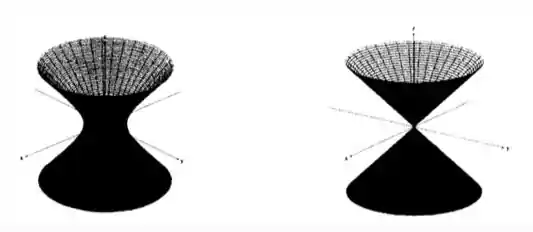
Segura que está quase! Vamos pra terceira superfície? Ela é:
Isso tá parecendo programa infantil: vamos, dee nooovo (ebaa \o/), zerar cada uma das variáveis!
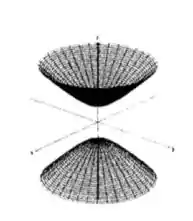
Zerando o , temos, no plano :
Opa, é uma hipérbole!
Agora, vamos zerar o ? Teremos, assim, no plano :
Ih, olha só, outra hipérbole! Meio na cara né... as únicas duas opções que temos são hiperboloides XD E agora? Só resta zerar a variável , né?
Fazendo isso, teremos:
Opa... calma aí, dois números ao quadrado, ainda por cima somados, dando um número negativo? Isso não pode acontecer no ! Sabe o que isso significa? Que nossa superfície não está definida no plano , ou seja, quando ! Daí sabemos que estamos falando do hiperboloide de duas folhas:
Perceba que, colocando , por exemplo, teríamos , ou seja, nossa curva de nível é uma circunferência de raio :D
Passo 6
Já dei um spoiler de que nossas curvas de nível serão circunferências né XD Mas, para não perder a rotina, temos que escolher, dentre as duas curvas que restam, a que obedeça à equação do hiperboloide:
Ou seja, que a terceira coordenada ao quadrado, seja a soma da primeira com a segunda, ambas ao quadrado, mais um :)
E a curva que nos fornece essa relação é:
Passo 7
Bom, agora que restou apenas a última superfície, vlw flws aí galera. Até a próxima questão!
Passo 8
Brincadeira XD Não vamos ficar na mão assim né? O RespondeAí vale cada centavo, cada questão :D
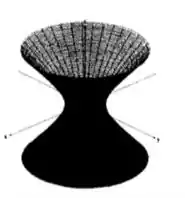
Vamos lá, qual será a diferença entre esse hiperboloide que temos agora e o outro? Se zerarmos , teremos, no plano :
Ou seja, uma hipérbole, assim como o outro...
Se zerarmos o , teremos no plano ,
Outra hipérbole! Até agora tudo igual né?
Mas, zerando , teremos, no plano ,
Uma circunferência! Viu? Quando cortamos nossa superfície pelo plano , temos alguma coisa palpável! Isso significa que a superfície existe em , e sua curva de nível é essa circunferência de raio . Por isso, temos um hiperboloide de uma folha, pois é uma superfície contínua e definida em todo o !
Passo 9
Agora, só vamos verificar que a curva de nível restante realmente pertence ao hiperboloide! Ela é:
E está sobre o hiperboloide , pois, colocando , temos que
E é uma solução para essa equação :D
Resposta