Seja
a) Esboce as curvas de nível de nos níveis e .
b) Existe ? Justifique.
Passo 1
a) Para ver as curvas de nível, temos apenas que igualar a função ao nível. Para o nível , teremos:
Agora, como sempre, vamos abrir tudo, juntar as variáveis e depois completar quadrados ;)
Passando tudo pro lado esquerdo, teremos:
Juntando as variáveis de mesmo grau, teremos:
Dividindo tudo por , temos:
Agora, completando o quadrado para o e para o , temos:
Que, fica:
Passo 2
Essa é a equação na qual chegamos é a da circunferência de raio , centrada em ! Seu esboço pode ser:
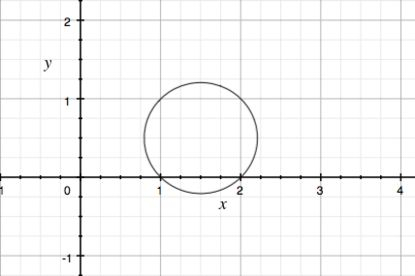
E é importante dizer que o domínio no qual estamos nessa curva de nível é:
Além disso o domínio da própria função vai ser quando o denominador for diferente de , ou seja
Isso nos diz que
Vamos ver se tem algum ponto desse domínio da curva de nível onde
A equação que tínhamos antes de arrumar tudo era
Vamos começar fazendo
Isso nos diz que
Então temos um ponto que temos que excluir desse domínio.
Vamos ver agora quando
Repara que nesse caso a solução vai ser complexa, isso porque
Então o nosso domínio só deveria excluir o ponto .
O domínio vai ser
O gráfico então vai ser
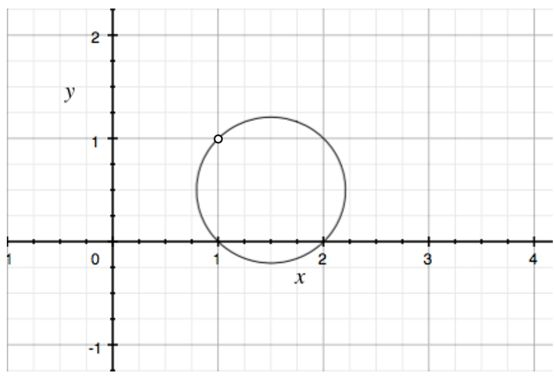
Passo 3
Vamos agora para o nível ? Se colocarmos , teremos:
Abrindo os parêntesis, teremos:
Cortando os e juntando os :
Multiplicando por e dividindo por pra ajeitar, teremos:
Passo 4
Essa equação que acabamos de encontrar é a de uma parábola! Ela está deitada, pois é função de . A boa está apontando para o sentido positivo de , pois o coeficiente de é positivo. Como estamos somando , ela é deslocada em , em relação à origem, no eixo . E, ainda, como temos , ela sobe ligeiramente em relação ao eixo :
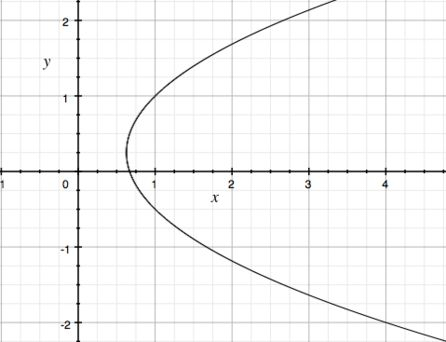
Assim, o domínio da nossa curva é:
Além disso o domínio da própria função vai ser quando o denominador for diferente de , ou seja
Isso nos diz que
Vamos ver se tem algum ponto desse domínio da curva de nível onde
Vamos começar fazendo
Isso nos diz que
Então temos um ponto que temos que excluir desse domínio.
Vamos ver agora quando
Repara que nesse caso a solução vai ser complexa, isso porque
Então o nosso domínio só deveria excluir o ponto .
O domínio vai ser
O gráfico da curva de nível vai ficar
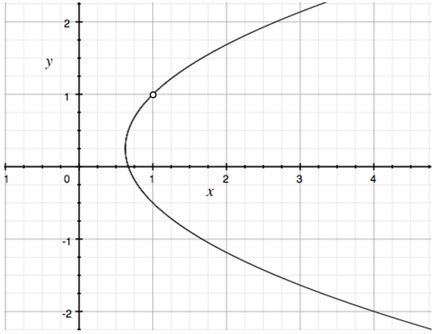
Passo 5
b) Beleza, agora temos que resolver
Como de costume, o primeiro passo é chutar (conscientemente) alguns caminhos para percorrermos esse limite, afim de encontrar dois valores diferentes e provar que ele não existe.
Se não conseguirmos provar que ele não existe, podemos partir para o teorema do sanduíche ;)
Por exemplo, podemos tentar fazer esse limite se igual a , tentando zerar o numerador sem zerar o denominador. Um caminho, por exemplo , faria a fração ficar:
Multiplicando por em cima e embaixo, teremos:
Sabendo que o denominador pode ser escrito como , teremos:
Cortando o de baixo com o de cima, temos:
Show! Encontramos um limite para a função, e deu .
Passo 6
Agora, vamos tentar encontrar outro limite, um que não dê , para provar que o limite não existe!
Antes de nos pedirem pra encontrar esse limite, nos pediram pra encontrar curvas de nível, certo? Isso está cheirando a “use as curvas de nível para ver se o limite existe ou não”! Não custa nada tentar, né? Vamos ver pela primeira, de nível . Ela era:
Parametrizando essa circunferência por coordenadas polares, tendo , e ,
Beleza?
Passo 7
Vamos agora jogar essa curva no limite pra função, colocando a primeira coordenada para o e a segunda para o :
Agora, não faz sentido resolver esse limite se não sabemos para qual valor o está tendendo! Pode ser que nem tenhamos uma indeterminação! Para isso, vejamos que valor de faz com que tenhamos, na circunferência, o ponto :
Igualando as primeiras coordenadas, temos:
E então, temos que ou .
Igualando as segundas coordenadas, teremos:
Ou seja, temos mesmo a primeira opção, :D
Passo 8
Colocando, agora, esse na equação do limite, teremos:
Vamos arrumar essa expressão gigante dentro do limite, primeiro vamos dar um jeito no numerador
Para deixar isso ainda mais arrumadinho vamos fazer
Vamos agora ao denominador
De novo vamos fazer
Repara que o numerador e o denominador ficaram iguais então nosso limite vai ser
Lembra que antes achamos o limite sendo ? Agora fazendo por outro caminho deu isso nos diz que o limite de não existe.
Resposta
a) Para : 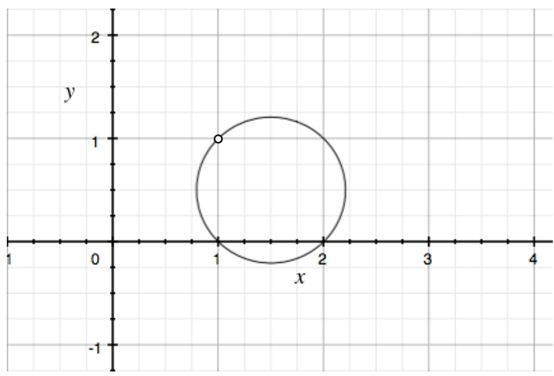
Para :
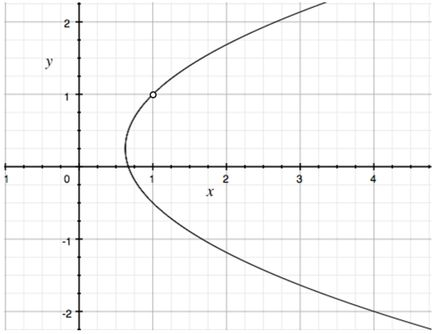
b) O limite não existe