Listas de Cálculo 2 - USP, Politécnica de Cálculo 2 da USP - Lista 1 - Polinômio de Taylor e Curvas Planas

Utilizando o polinômio de Taylor de ordem , calcule um valor aproximado e avalie o erro.

a)

Utilizando o polinômio de Taylor de ordem , calcule um valor aproximado e avalie o erro.

b)

Utilizando o polinômio de Taylor de ordem , calcule um valor aproximado e avalie o erro.

c)

Mostre que

a)

Mostre que

b)

Determine o polinômio de Taylor de ordem da função em torno de .

Determine , o polinômio de Taylor de ordem da função em torno de e dê a fórmula para o erro . Use esse polinômio com um conveniente para avaliar com erro inferior a .

(a) Seja um inteiro ímpar. Mostre que:

(b) Avalie com erro inferior a .

(a) Determine o polinômio de Taylor de ordem da função em torno de .

(b) Avalie com erro, em módulo, inferior a .

c. Mostre que , .

d. Avalie com erro inferior a .

Seja uma função de classe e suponha que seja um ponto crítico de . Mostre que:

b. se , então é um ponto de máximo local de ;

Sejam I um intervalo aberto e uma função vezes derivável em I, onde . Suponha que exista um polinômio

tal que

.

Deduza quem são os coeficientes de .

Sejam uma função infinitamente derivável, um número real fixado e, para cada o polinômio de Taylor de ordem de em torno de . Seja ainda o erro cometido na aproximação de por . Verifique se as afirmações abaixo são verdadeiras ou falsas. Justifique.

é o único polinômio que satisfaz.

.

Sejam uma função infinitamente derivável, um número real fixado e, para cada o polinômio de Taylor de ordem de em torno de . Seja ainda o erro cometido na aproximação de por . Verifique se as afirmações abaixo são verdadeiras ou falsas. Justifique.

Para todo temos

.

Sejam uma função infinitamente derivável, um número real fixado e, para cada o polinômio de Taylor de ordem de em torno de . Seja ainda o erro cometido na aproximação de por . Verifique se as afirmações abaixo são verdadeiras ou falsas. Justifique.

Se , então .

Sejam uma função infinitamente derivável, um número real fixado e, para cada o polinômio de Taylor de ordem de em torno de . Seja ainda o erro cometido na aproximação de por . Verifique se as afirmações abaixo são verdadeiras ou falsas. Justifique.

Se , para todo , então

.

Use o seguinte roteiro para provar que é irracional.

Use a Fórmula de Taylor com resto de Lagrange para provar que, para cada número inteiro temos

,

onde satisfaz .

Use o seguinte roteiro para provar que é irracional.

Suponha, por absurdo, que seja racional e escreva , onde são inteiros positivos. Escolha um número inteiro tal que e . Use o item anterior para concluir que

Use o seguinte roteiro para provar que é irracional.

Reescreva a igualdade acima para obter

Use o seguinte roteiro para provar que é irracional.

Mostre que cada termo do lado direito da igualdade acima é um número inteiro (aqui a desigualdade será crucial). Deduza que também é inteiro.

Use o seguinte roteiro para provar que é irracional.

Usando as desigualdades e , mostre que . Obtenha uma contradição e conclua que não pode ser racional.

Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:

a. ;

Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:

b. ;

Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:

c. ;

Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:

d. ;

Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:

e. ;

Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:

f. ;

Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:

g. ;

Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:

h. ;

Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:

i. ;

Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:

j. ;

Esboce e parametrize cada conjunto como uma curva:

Esboce e parametrize cada conjunto como uma curva:

Esboce e parametrize cada conjunto como uma curva:

Esboce e parametrize cada conjunto como uma curva:

sendo e a reta .

Esboce e parametrize cada conjunto como uma curva:

sendo e .

Esboce e parametrize cada conjunto como uma curva:

com e .

Seja uma função de classe e suponha que seja um ponto crítico de . Mostre que:

a.se , então é um ponto de mínimo local de ;

Considere

a. Mostre que a função f não é derivável em .

Considere

b. Determine uma curva , derivável e cuja imagem seja igual ao gráfico de .

Considere

c. Interprete geometricamente o fato de que f não é derivável em x = 0, mas a curva γ é derivável em , onde .

Sejam I um intervalo aberto de R e uma curva diferenciável. Mostre que, se existe C ∈ R tal que , para todo t ∈ I, então γ(t) é ortogonal a γ’ (t), para todo t ∈ I. Vale a recíproca? Interprete geometricamente.

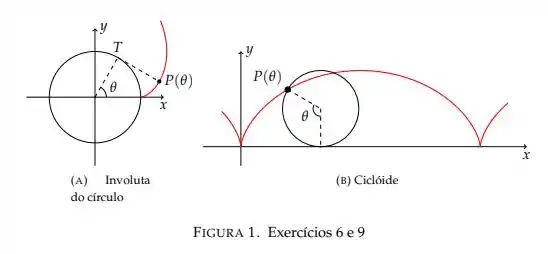
Um barbante é enrolado ao redor de um círculo e então desenrolado, sendo mantido esticado. A curva traçada pelo ponto P no final do barbante é chamada de involuta do círculo. Se o círculo tiver raio r e centro O, a posição inicial de P for (r, 0), e se o parâmetro θ for escolhido como na Figura 1(a), mostre que as equações paramétricas da involuta são:

e

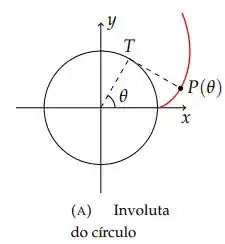
Considere a curva plana dada por

Esboce a imagem da curva e o sentido do percurso. Sugestão: tente calcular em alguns pontos e ver se consegue visualizar a curva e o sentido do percurso, depois cheque usando algum aplicativo: desmos ou wolframalpha ou outro. O nome dessa curva é “caridióide” - você vai entender a razão!

Considere a curva plana dada por

O ponto mais à direita da curva é…

Considere a curva plana dada por

O ponto mais alto da curva é…

Considere a curva plana dada por

O ponto mais baixo da curva é…

Considere a curva plana dada por

Quais das curvas abaixo têm a mesma imagem que a curva ?

Considere a curva plana dada por

Qual o ponto da curva mais próximo da origem? E o mais distante?

Uma circunferência de raio rola sem escorregar ao longo do eixo . Encontre equações paramétricas para a curva descrita por um ponto da circunferência que se encontra inicialmente na origem. (Esta curva é chamada ciclóide, veja a Figura 1(b))

Considere a curva dada por . Sabe-se que a imagem de admite, no ponto , dois vetores tangentes, unitários e com produto escalar positivo. Determine o valor desse produto escalar.

Considere as seguintes afirmações:

A imagem da curva está contida em uma reta.

A imagem da curva é uma parábola.

A imagem da curva está contida em uma hipérbole.

São corretas apenas as afirmações

Considere a curva plana dada por

O ponto mais à esquerda da curva é…

Mostre que a curva tem duas tangentes em (0, 0) e ache suas equações. Faça um esboço da curva.

Seja f : R → R uma função derivável até quarta ordem tal que f(0) = 3, f'(0) = −2, f''(0) =2 e f'''(0) = 4. Suponha que

, para todo x ∈ R. Obtenha uma aproximação com cinco casas decimais para f(1/3) e determine o erro cometido nessa aproximação.