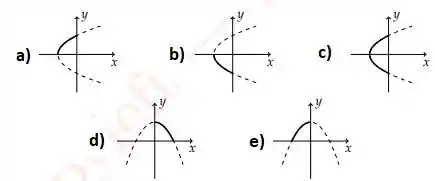P1 de Cálculo 2 da USP - 2019

Dentre as figuras abaixo aquelas que associam corretamente e superfície são:

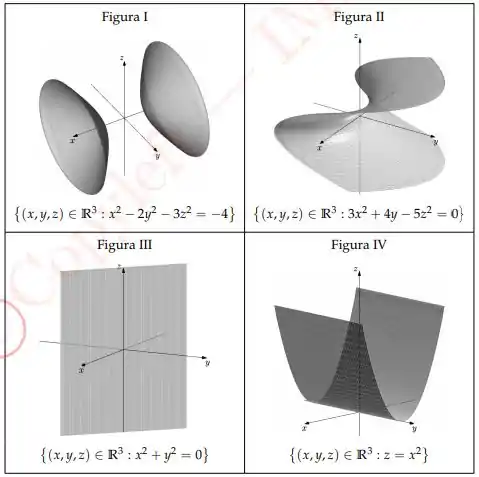
a) II e IV.

b) I e II.

c) I e III.

d) III e IV.

e) I e IV.

Considere a função

Então

a) a curva de nível de está contida em uma hipérbole.

b) a curva de nível de é uma elipse.

c) a curva de nível de é uma parábola.

d) a curva de nível de está contida em uma elipse.

e) a curva de nível de é um conjunto vazio.

Considere a função

Então

a) a curva de nível de está contida em uma elipse.

b) a curva de nível de é uma hipérbole.

c) a curva de nível de está contida em uma elipse.

d) a curva de nível de é uma parábola.

e) a curva de nível de é um conjunto vazio.

Considere a função

É correto afirmar que o domínio de contém

a) a parábola .

b) a hipérbole .

c) a reta .

d) o círculo .

e) a elipse .

Considere a função

É correto afirmar que o domínio de contém

a) a hipérbole .

b) a reta .

c) o círculo .

d) a elipse .

e) a parábola .

Considere a função

É correto afirmar que o domínio de contém

a) o círculo .

b) a hipérbole .

c) a reta .

d) a elipse .

e) a parábola .

Considere a função

É correto afirmar que o domínio de contém

a) a elipse .

b) a hipérbole .

c) a reta .

d) o círculo .

e) a parábola .

Considere a função

Então

a) a curva de nível de está contida em uma parábola.

b) a curva de nível de é uma elipse.

c) a curva de nível de é uma hipérbole.

d) a curva de nível de está contida em uma elipse.

e) a curva de nível de é um conjunto vazio.

A reta tangente à curva dada pela intersecção das superfícies e no ponto é paralela ao vetor

a) .

b) .

c) .

d) .

e) .

A reta tangente à curva dada pela intersecção das superfícies e no ponto é paralela ao vetor

a) .

b) .

c) .

d) .

e) .

Considere a função definida por

Então

a) não é contínua no ponto .

b) a curva de nível contem o ponto .

c) existe o limite , mas não é contínua nesse ponto.

d) é contínua no ponto .

e) é contínua no ponto .

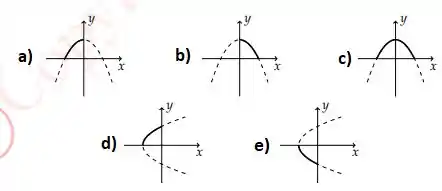
Dentre as figuras abaixo aquelas que associam corretamente e superfície são:

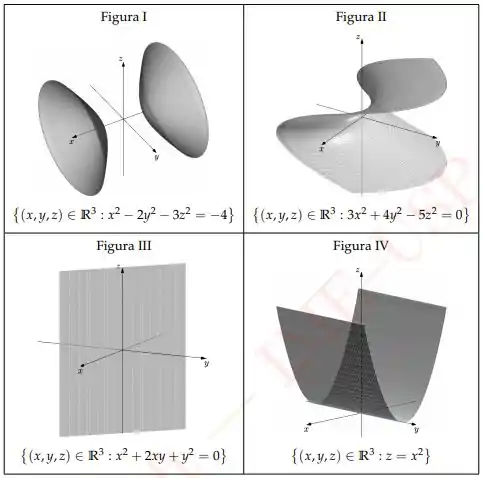
a) III e IV.

b) I e II.

c) I e III.

d) II e IV.

e) I e IV.

Considere a função definida por

Então

a) não é contínua no ponto .

b) a curva de nível contem o ponto .

c) existe o limite , mas não é contínua nesse ponto.

d) é contínua no ponto .

e) é contínua no ponto .

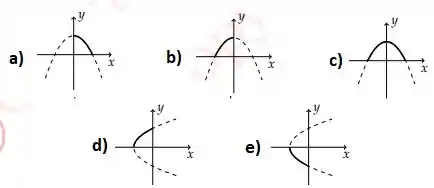
Dentre as figuras abaixo aquelas que associam corretamente e superfície são:

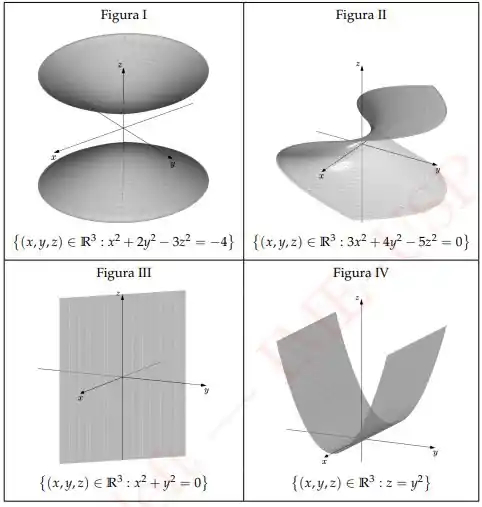
a) I e IV.

b) I e II.

c) I e III.

d) II e IV.

e) III e IV.

A reta tangente à curva dada pela intersecção das superfícies e no ponto é paralela ao vetor

a) .

b) .

c) .

d) .

e) .

Considere a função definida por

Então

a) não é contínua no ponto .

b) a curva de nível contem o ponto .

c) existe o limite , mas não é contínua nesse ponto.

d) é contínua no ponto .

e) é contínua no ponto .

A imagem da curva , está melhor representada em

A imagem da curva , está melhor representada em

A imagem da curva , está melhor representada em

A imagem da curva , está melhor representada em

Uma parametrização para a intersecção dos gráficos das funções e , em que , é dada por

em que , , e são número reais positivos.

Então, é igual a

a) .

b) .

c).

d) .

e) .

Uma parametrização para a intersecção dos gráficos das funções e , em que , é dada por

em que , , e são número reais positivos.

Então, é igual a

a) .

b) .

c).

d) .

e) .

Uma parametrização para a intersecção dos gráficos das funções e , em que , é dada por

em que , , e são número reais positivos.

Então, é igual a

a) .

b) .

c).

d) .

e) .

Uma parametrização para a intersecção dos gráficos das funções e , em que , é dada por

em que , , e são número reais positivos.

Então, é igual a

a) .

b) .

c).

d) .

e) .

Considere a função

para todo e . O valor do limite é

a) .

b) .

c) .

d) .

e) inexistente.

Suponha que a imagem da curva está contida na curva de nível da função , em que . Então, a reta tangente a em é

a) .

b) .

c) .

d) .

e) .

Considere a função

para todo e . O valor do limite é

a) .

b) .

c) .

d) .

e) inexistente.

Considere a função

para todo e . O valor do limite é

a) .

b) .

c) .

d) .

e) inexistente.

Considere a função

para todo e . O valor do limite é

a) .

b) .

c) .

d) .

e) inexistente.

Suponha que a imagem da curva está contida na curva de nível da função , em que . Então, a reta tangente a em é

a) .

b) .

c) .

d) 7.

e) .

Suponha que a imagem da curva está contida na curva de nível 3 da função , em que . Então, a reta tangente a em é

a) .

b) .

c) .

d) .

e) .

Suponha que a imagem da curva está contida na curva de nível da função , em que . Então, a reta tangente a em é

a) .

b) .

c) .

d) 7.

e) .