PF de Física 1 da UFRJ - 2015.2
Física 1 - UFRJ
Um bloco de massa m desce de uma distância d ao longo de uma superfície plana inclinada, fixa ao solo, que faz um ângulo θ com a horizontal. O coeficiente de atrito cinético entre o bloco e a superfície vale µc. Os trabalhos realizados pelas forças gravitacional, normal e força de atrito valem, respectivamente:
(a) +mgd sen θ, 0, −µcmgd cos θ
(b) +mgd cos θ, 0, −µcmg dsen θ
(c) +mgd sen θ, 0, +µcmgd cos θ
(d) −mgd sen θ, −mgd sen θ, −µcmgd cos θ
(e) −mgd sen θ, −mgd, +µcmgd cos θ
(f) +mgd sen θ, mgd, −µcmgd sen θ
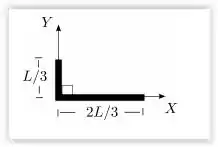
Ver solução completaO momento de inércia de uma barra homogênea de massa m e comprimento l em relação a um eixo que passa por uma de suas extremidades e é perpendicular a ela é . Uma barra homogênea de comprimento L e massa M é dobrada a uma distância L/3 de uma de suas extremidades, como mostra a figura. O momento de inércia desta configuração em relação ao eixo Oy é:
Um reservatório de massa total M pode ser representado por uma caixa cúbica, oca, de paredes finas e homogêneas de lado L. O reservatório está parcialmente cheio por um líquido de densidade volumétrica uniforme ρ. Sabendo que a coluna do líquido no interior do reservatório tem altura h, a altura do centro de massa do conjunto reservatório + líquido em relação à base do reservatório é:
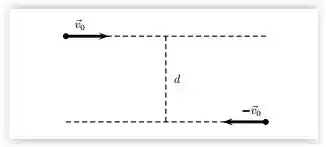
Dois patinadores de mesma massa m aproximam-se um do outro em trajetórias paralelas separadas por uma distância d, como mostrado na figura. Eles possuem velocidades de mesmo módulo . Quando passam um pelo outro, dão-se as mãos, mantendo a distância de d entre eles. Em um certo instante, os dois patinadores se puxam encurtando a distância entre eles que passa a ser , e assim permanecem. Nesta situação final, qual é a velocidade angular de rotação do sistema em torno de seu centro de massa?
- 0
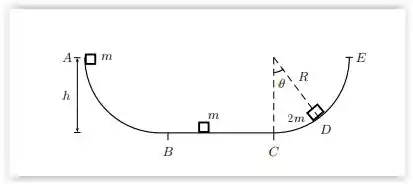
A figura mostra um circuito ABCDE de atrito desprezível, com um trecho horizontal BC, um arco de círculo CE de raio R e o ponto A a uma altura h do trecho horizontal. Um bloco de massa m é abandonado em repouso no ponto A e um bloco idêntico está em repouso sobre o circuito entre B e C. O bloco abandonado em A sofre uma colisão perfeitamente inelástica, com os blocos permanecendo unidos após a colisão. Calcule:
- a velocidade do bloco abandonado em A imediatamente antes de colidir com o outro bloco;
- a velocidade do conjunto imediatamente depois da colisão;
- a velocidade do conjunto no ponto D, onde a direção da normal faz um ângulo θ = 60◦ com a vertical (Supondo que a altura h seja suficiente para que os blocos passem por esse ponto com velocidade não nula);
- o valor da força normal que age sobre os dois blocos grudados, no ponto D.
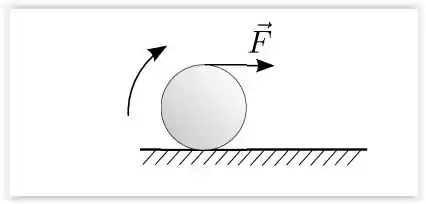
Um disco homogêneo de massa M e raio R encontra-se em repouso sobre uma superfície plana, horizontal e com atrito. Num dado instante, ele é puxado por um fio ideal que está enrolado em sua periferia, como mostrado na figura. A força exercida pelo fio e horizontal e tem módulo F constante. Sabe-se que o disco rola para a direita, sem deslizar sobre a superfície, e que seu momento de inércia em relação a um eixo perpendicular ao plano do disco e que passa pelo seu centro é .
- Faça um diagrama representando todas as forças que agem sobre o disco nos seus respectivos pontos de aplicação;
b) Calcule o módulo da aceleração do centro de massa do disco;
- Determine a força de atrito que age sobre o disco (módulo, direção e sentido).
Uma partícula executa um movimento pendular num plano vertical xy, oscilando entre duas posições extremas A e B, como mostra a figura. Considerando o trajeto A → B pode-se afirmar que:
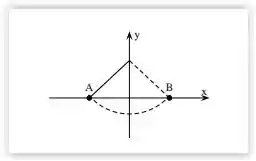
(a) o vetor velocidade média entre A e B tem a direção e o sentido do eixo x positivo
(b) o vetor velocidade média entre A e B tem a direção e o sentido do eixo x negativo
(c) nos pontos A e B a aceleração é nula
(d) o vetor velocidade média entre A e B é nulo
(e) o vetor aceleração média entre A e B tem a direção e sentido do eixo y positivo
Ver solução completaUm cilindro de massa rola sem deslizar sobre um plano horizontal rugoso com velocidade angular constante. O coeficiente de atrito estático entre o plano e o cilindro é . Seja o módulo da força de atrito estático entre o cilindro e a superfície, e , as energias cinética de rotação e translação do cilindro, respectivamente. Sabendo que o momento de inércia de um cilindro relativo ao seu eixo de simetria perpendicular às bases é , é correto afirmar que:
(a) e
(b) e
(c) e
(d) e
(e) e
(f) e
Ver solução completaUm bloco encontra-se em equilíbrio suspenso por uma mola de constante elástica , presa ao teto e com alongamento . O bloco é levantado até a posição em que a alongação é nula e abandonado a partir do repouso. Ao descer uma altura o bloco ganha uma energia cinética igual a:
A figura mostra a energia potencial U(x) de uma partícula que se move ao longo do eixo x sob a ação da força resultante associada a U(x). Sabendo-se que a energia mecânica E é maior que U() e menor que U(), a alternativa FALSA é:
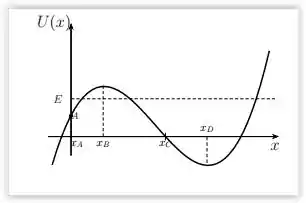
- o sentido da força na posição é positivo
- o sentido da força na posição é positivo
- na posição a força é nula
- caso a partícula passe pela posição , sua energia cinética nesse ponto é máxima
- a partícula não pode estar na posição
- caso a partícula passe pelo ponto , no deslocamento do ponto para o ponto , o trabalho realizado pela força é positivo.
(b) na posição a força é nula
(c) caso a partícula passe pela posição , sua energia cinética nesse ponto é máxima
(d) a partícula não pode estar na posição
(e) caso a partícula passe pelo ponto , no deslocamento do ponto para o ponto , o trabalho realizado pela força é positivo
Passo 1
Vamos analisar cada uma das afirmativas:
Começando pela primeira alternativa:
A gente sabe da relação entre força externa e energia potencial:
Na posição , nós vemos que a derivada do gráfico é positiva, logo é negativa, o que implica num sentido negativo.
Afirmativa é falsa.
Passo 2
Vamos aplicar novamente
No caso da posição , a derivada é nula, logo .
Afirmativa verdadeira,
Passo 3
Vamos entender essa afirmativa por meio do conceito de conservação da energia mecânica. A energia potencial se transforma em energia cinética e vice-versa, mas a soma das duas que é a energia total do sistema se conserva.
No ponto , a partícula está no ponto mínimo de energia potencial, logo é o ponto de energia cinética máxima.
Afirmativa verdadeira.
Passo 4
A energia mecânica total de se um sistema se dá pela soma da energia cinética com a energia potencial.
A energia potencial do ponto é maior do que a energia mecânica total, o que não pode acontecer devido à equação mostrada acima.
Afirmativa verdadeira.
Passo 5
Pelo teorema trabalho energia cinética, a gente sabe que:
Já vimos também quanto maior a energia potencial, menor a energia cinética, logo no ponto a energia cinética é menor do que no ponto .
Assim, sabemos que e, portanto, o trabalho é positivo.
Afirmativa verdadeira.
Ver solução completa