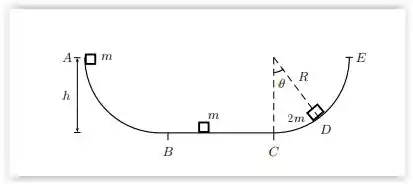
A figura mostra um circuito ABCDE de atrito desprezível, com um trecho horizontal BC, um arco de círculo CE de raio R e o ponto A a uma altura h do trecho horizontal. Um bloco de massa m é abandonado em repouso no ponto A e um bloco idêntico está em repouso sobre o circuito entre B e C. O bloco abandonado em A sofre uma colisão perfeitamente inelástica, com os blocos permanecendo unidos após a colisão. Calcule:
- a velocidade do bloco abandonado em A imediatamente antes de colidir com o outro bloco;
- a velocidade do conjunto imediatamente depois da colisão;
- a velocidade do conjunto no ponto D, onde a direção da normal faz um ângulo θ = 60◦ com a vertical (Supondo que a altura h seja suficiente para que os blocos passem por esse ponto com velocidade não nula);
- o valor da força normal que age sobre os dois blocos grudados, no ponto D.
Passo 1
Primeiramente, vamos entender melhor o problema.
Podemos ver que as forças que atuam sobre o bloco no trecho AB são apenas o peso e a normal.
Como a Normal é sempre perpendicular à trajetória, o trabalho devido a ela neste trajeto é nulo. Além disso, o peso é uma força conservativa.
Então, podemos aplicar a lei de conservação da energia mecânica entre os pontos A e B.
Vamos analisar cada uma dessas energias:
. O bloco é solto do repouso
Chegamos, então, a
Manipulando essa equação:
Passo 2
Como a soma das forças externas é nula, podemos aplicar a lei da conservação do momento linear para os instantes antes e depois da colisão.
Vamos analisar cada momento linear separadamente:
será dado só pelo bloco que estava em movimento, já que o bloco em repouso tem sem momento linear nulo.
Assim, como achamos a velocidade do primeiro bloco imediatamente antes de colidir no passo anterior, chegamos a:
Para calcular o , vamos utilizar o fato de que se trata de uma colisão completamente inelástica, ou seja, os dois blocos saem juntos após a colisão.
Dessa forma, podemos analisar o momento linear do sistema de massa 2m com velocidade única (, formado pelos dois blocos.
Assim,
Igualando os dois resultados,
Passo 3
Agora precisamos encontrar .
Vamos aplicar novamente a lei de conservação da energia mecânica no trecho CD.
Vamos analisar separadamente cada uma dessas energias:
, sendo a velocidade do conjunto em c igual ao calculado no passo 2
Precisamos descobrir qual o valor de . Para isso vamos montar a seguinte figura:
Show! Agora é só igualar tudo.
Dando uma arrumadinha nisso aí, chegamos no módulo de :
Passo 4
Vamos entender quais as forças que atuam no ponto D.
Como o bloco faz um movimento circular, ele tem uma força centrípeta. Conforme vemos na figura, essa força centrípeta vai ser dada por . No nosso caso,
Nós já sabemos que a é dada por . Assim, podemos aplicar para nosso conjunto de 2m no ponto D.
Substituindo na primeira equação, chegamos a: