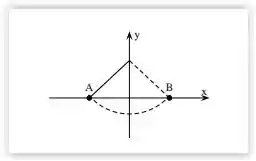
Uma partícula executa um movimento pendular num plano vertical xy, oscilando entre duas posições extremas A e B, como mostra a figura. Considerando o trajeto A → B pode-se afirmar que:

(a) o vetor velocidade média entre A e B tem a direção e o sentido do eixo x positivo

(b) o vetor velocidade média entre A e B tem a direção e o sentido do eixo x negativo

(c) nos pontos A e B a aceleração é nula

(d) o vetor velocidade média entre A e B é nulo

(e) o vetor aceleração média entre A e B tem a direção e sentido do eixo y positivo

Vamos pensar na velocidade nesse trajeto:

Ou seja é a variação da posição da partícula dividida pelo tempo. Como estamos analisando o vetor velocidade média, ele só depende da diferença de posição.

Vemos que é positivo, logo está orientado no sentido positivo de x.

Ficou confuso?

Dá uma olhada na figura abaixo:

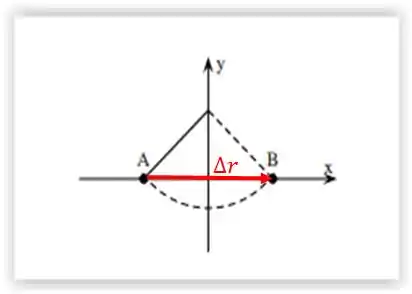
Esse é o vetor que ilustra a variação do vetor posição. (direção e sentido do eixo x positivo)

Às vezes uma imagem realmente vale mais do que mil palavras.