Um bloco de massa m desce de uma distância d ao longo de uma superfície plana inclinada, fixa ao solo, que faz um ângulo θ com a horizontal. O coeficiente de atrito cinético entre o bloco e a superfície vale µc. Os trabalhos realizados pelas forças gravitacional, normal e força de atrito valem, respectivamente:
(a) +mgd sen θ, 0, −µcmgd cos θ
(b) +mgd cos θ, 0, −µcmg dsen θ
(c) +mgd sen θ, 0, +µcmgd cos θ
(d) −mgd sen θ, −mgd sen θ, −µcmgd cos θ
(e) −mgd sen θ, −mgd, +µcmgd cos θ
(f) +mgd sen θ, mgd, −µcmgd sen θ
Passo 1
Vamos entender, primeiro, a situação do plano inclinado:
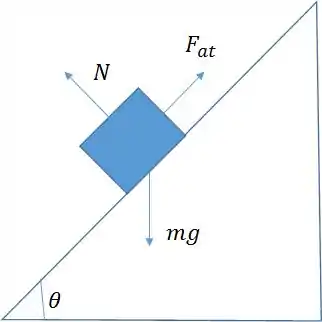
Passo 2
Agora, vamos aplicar o conceito de trabalho para cada uma das forças.
Começando pelo trabalho realizado pela força gravitacional, ou seja, a força peso:
Para isso vamos achar a componente do peso que atua na direção do deslocamento, pela figura:
Logo,
Passo 3
Vamos analisar agora o trabalho da normal. Podemos que a normal tá sempre perpendicular ao deslocamento, logo:
Como , chegamos a:
Passo 4
Vamos analisar o trabalho da força de atrito.
Primeiro, sabemos que
Podemos também achar a normal pela outra componente do peso que achamos pela figura da mesma que a do passo 2:
Show!
Por fim, aplicamos a fórmula do trabalho:
Só precisamos ter atenção com esse sinal negativo, mas isso faz bastante sentido! A força de atrito tá num sentido contrário que o deslocamento.
Resposta
(a) +mgd sen θ, 0, −µcmgd cos θ