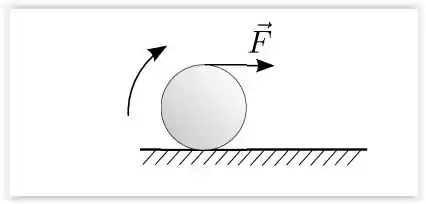
Um disco homogêneo de massa M e raio R encontra-se em repouso sobre uma superfície plana, horizontal e com atrito. Num dado instante, ele é puxado por um fio ideal que está enrolado em sua periferia, como mostrado na figura. A força exercida pelo fio e horizontal e tem módulo F constante. Sabe-se que o disco rola para a direita, sem deslizar sobre a superfície, e que seu momento de inércia em relação a um eixo perpendicular ao plano do disco e que passa pelo seu centro é .
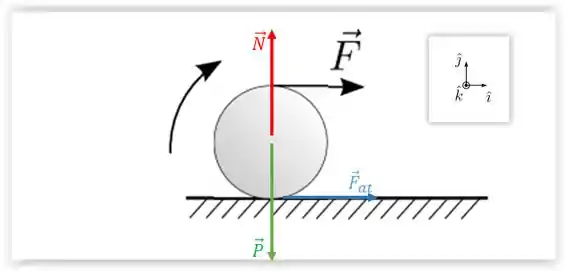
- Faça um diagrama representando todas as forças que agem sobre o disco nos seus respectivos pontos de aplicação;
b) Calcule o módulo da aceleração do centro de massa do disco;
- Determine a força de atrito que age sobre o disco (módulo, direção e sentido).
Passo 1
Primeiramente, vamos marcar as forças:
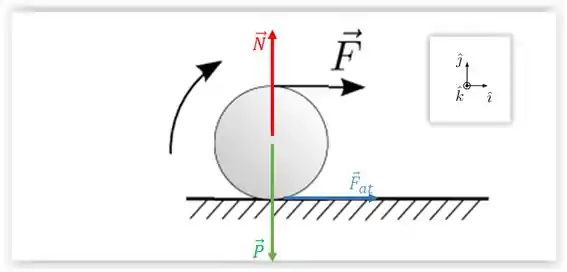
é a força aplicada sobre o disco
é a força peso
é a força normal
é a força de atrito
Passo 2
Sabemos que a dinâmica do disco é descrita pela combinação de dois modos de movimento: translação e rotação, vamos analisar melhor cada um deles.
Translação:
Rotação:
Como o enunciado fala que o disco rola sem deslizar, podemos utilizar o vínculo entre a aceleração do centro de massa e a aceleração angular, dado por:
Para a translação, temos duas equações se considerarmos os sentidos das forças.
Em x temos:
Em y temos:
Para rotação, vamos calcular os torques em relação ao centro do disco. Dessa forma, os torques gerados pela força peso e pela força normal serão nulos, visto que a linha de ação de ambas as forças passa pelo eixo de rotação.
Considerando o sentido anti-horário como positivo e sendo R a distância da linha de ação das forças e até o eixo de rotação, montamos:
É possível percebermos que é negativo por estar no sentido horário.
Show!
Agora, lembrando do vínculo: e da equação que montamos em x para a translação e da equação da rotação, podemos montar o seguinte sistema:
Resolvendo esse sistema:
Como o enunciado nos forneceu o valor do momento de inércia , chegamos a:
Passo 3
Precisamos achar a
Para isso vamos usar a equação que montamos no passo anterior do movimento de translação na horizontal:
Podemos substituir pelo valor encontrado também no passo anterior:
Chegamos então a:
O fato do sinal ser positivo mostra que arbitramos a força de atrito no sentido correto inicialmente. Caso o sinal fosse negativo, a força de atrito apontaria para esquerda.
Portanto, chegamos a: