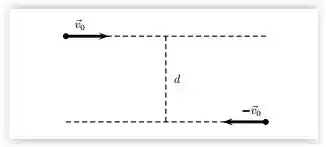
Dois patinadores de mesma massa m aproximam-se um do outro em trajetórias paralelas separadas por uma distância d, como mostrado na figura. Eles possuem velocidades de mesmo módulo . Quando passam um pelo outro, dão-se as mãos, mantendo a distância de d entre eles. Em um certo instante, os dois patinadores se puxam encurtando a distância entre eles que passa a ser , e assim permanecem. Nesta situação final, qual é a velocidade angular de rotação do sistema em torno de seu centro de massa?
- 0
Passo 1
Vamos entender primeiro o que está acontecendo. Os patinadores giravam a uma distância entre si e depois diminuíram para uma distância . Precisamos descobrir a velocidade angular do sistema em torno do seu centro de massa, sendo o de cada um dado.
Como as forças externas do problema são apenas peso e normal e ambas se anulam em cada patinador, podemos dizer que , ou seja, o somatório das forças resultantes é igual a zero.
Assim, podemos utilizar a conservação do momento angular:
Passo 2
Vamos analisar primeiramente.
O módulo do momento angular antes dos dois patinadores darem a mão em relação ao centro de massa é dado por:
Como r é a distância do patinador ao centro de massa, ele vale ;
Assim, chegamos que a soma do momento angular dos dois patinadores é:
Passo 3
Vamos analisar o .
Nesse caso, temos dois patinadores girando juntos, logo teremos uma massa total de . Além disso, a distância entre os dois encurtou para e, por consequência, r (distância até o centro de massa) passa a valer .
Aplicando o momento angular do sistema formado pelos dois patinadores:
Passo 4
Igualando os dois momentos, chegamos a:
Passo 5
Mas a resposta está pedindo a velocidade angular e esse v que achamos é a velocidade linear. Você lembra dessa relação?
Então, vamos aplica-la para descobrirmos a velocidade angular, lembrando que o raio vale :