Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema dos Eixos Paralelos

Ver Teoria
Exercício 1512345678910111213141617181920212223242526272829

Enunciado

UFRJ, Física 1, Prova Final, 2015.2

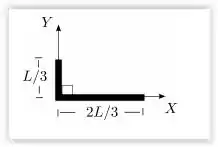
O momento de inércia de uma barra homogênea de massa m e comprimento l em relação a um eixo que passa por uma de suas extremidades e é perpendicular a ela é m l 2 3 . Uma barra homogênea de comprimento L e massa M é dobrada a uma distância L/3 de uma de suas extremidades, como mostra a figura. O momento de inércia desta configuração em relação ao eixo Oy é:

  1. 8 M L 2 81
  2. 4 M L 2 81
  3. 4 M L 27
  4. M L 2 27
  5. M L 2 3
  6. M L 2 9

Passo 1

Como ele quer o momento de inércia em relação ao eixo Oy e o momento de inércia que passa pela extremidade foi dado, faz muito sentido dividirmos essa “barra em L” em duas barras retas.

Então é isso, dividirmos a barra de questão em duas:

Uma de comprimento L 3 e outra de comprimento 2 L 3 , calculamos cada momento de inércia da extremidade e somamos.

Passo 2

A barra de de comprimento L 3 está sempre passando pelo eixo y, logo não gerará momento de inércia em relação a esse eixo.

Lembrando a fórmula de momento de inércia:

I = M R 2

Onde R é a distância da partícula/ ponto de um corpo extenso até o eixo de rotação.

Como R é sempre zero para esse caso, o momento de inércia gerado por essa barra é nulo.

I b a r r a 1 = 0

Passo 3

Agora analisaremos a barra maior. Nesse caso, o R (distância de um ponto da barra até o eixo) varia e não é nulo, logo teremos momento de inércia. O comprimento da barra é de 2 L 3 e, como a distribuição de massa é uniforme, ela tem um valor de massa de 2 M 3 .

Além disso, temos que lembrar que o momento de inércia de uma barra de comprimento l e massa m em relação a um eixo que passa por uma de suas extremidades e é perpendicular a ela é dado no enunciado por:

I b a r r a = m l 2 3

Como no nosso caso m = 2 M 3 e l = 2 L 3 , aplicando na fórmula:

I b a r r a 2 = m l 2 3 = 2 M 3 2 L 3 2 1 3

I b a r r a 2 = 2 M 3 4 L 2 9 1 3

I b a r r a 2 = 8 M L 2 81      

Passo 4

Somando os dois valores para termos o momento de inércia do sistema da Barra L, formado pelas duas barras, chegamos a:

I s i s = I b a r r a 1 + I b a r r a 2

I s i s = 0 + 8 M L 2 81

Resposta

  1. 8 M L 2 81

Exercícios de Livros Relacionados

Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
Um disco uniforme de raio r e massa M gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano ve
Usando o teorema dos eixos paralelos e informações da Tabela 9.2, ache o momento de inércia da barra delgada de massa M e comprimento L indicado na Figura 9.23 em relação a um eixo passando pelo ponto
Uma barra delgada de comprimento L possui massa por unidade de comprimento variando a partir da extremidade esquerda, onde x = 0 , de acordo com d m / d x = γ x , onde γ é constante com unidades de k
Use a Equação (9.20) para calcular o momento de inércia de um disco maciço, uniforme, de raio R e massa M em relação a um eixo perpendicular ao plano do disco passando pelo seu centro.