A figura mostra as curvas obtidas em três experimentos diferentes para o deslocamento horizontal em relação à posição de equilíbrio, , de um mesmo sistema bloco-mola que oscila descrevendo um movimento harmônico simples. Qual alternativa é correta?

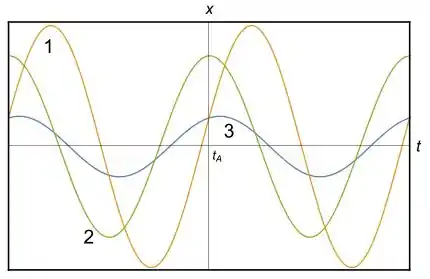
(a) Em , o módulo da aceleração do bloco no experimento 2 é menor que no experimento 1 e maior que no experimento 3.

(b) Em , a energia potencial elástica no experimento 1 é maior que a energia potencial elástica nos experimentos 2 e 3, sendo a energia potencial elástica no experimento 3 menor que no experimento 2.

(c) Em , o módulo da velocidade do bloco no experimento 1 é maior que nos experimentos 2 e 3.

(d) A freqüência angular do sistema nos três experimentos é diferente.

(e) Em , a energia cinética do bloco no experimento 2 é maior que no experimento 3.

Se olharmos o ponto , temos que .

Como a energia potencial elástica (U) é calculada como

Daí dá pra tirar que a energia potencial vai ser .

Logo, (b) Em , a energia potencial elástica no experimento 1 é maior que a energia potencial elástica nos experimentos 2 e 3, sendo a energia potencial elástica no experimento 3 menor que no experimento 2, está errada.

Se pensarmos agora em velocidade, que é a inclinação da reta tangente naquele ponto, no caso , tem a maior inclinação, seguida de , e .

Logo, , o que faz com que a alternativa correta seja (c) Em , o módulo da velocidade do bloco no experimento 1 é maior que nos experimentos 2 e 3.

Para excluir as outras alternativas, a energia cinética (K) é

Logo, . Então (e) Em , a energia cinética do bloco no experimento 2 é maior que no experimento 3 está errada.

E como a aceleração no MHS é

Então , assim, (a) Em , o módulo da aceleração do bloco no experimento 2 é menor que no experimento 1 e maior que no experimento 3 também está errada.