Um pêndulo formado por uma esfera de massa e raio desprezível está suspenso verticalmente a partir do ponto através de uma haste rígida de massa desprezível e comprimento . A haste está ligada a duas molas idênticas de constantes elásticas , massas desprezíveis, situadas a uma distância de como mostrado na figura (a). As molas estão relaxadas (isto é nem esticadas, nem comprimidas) quando o pêndulo está na posição vertical. Para iniciar o balanço do pêndulo, você o desloca com as mãos até que a haste forme um pequeno ângulo com a vertical, liberando-o a partir do repouso [figura (b)].
Dica: como o ângulo é pequeno, considere que as molas permanecem essencialmente na horizontal durante todo o movimento.
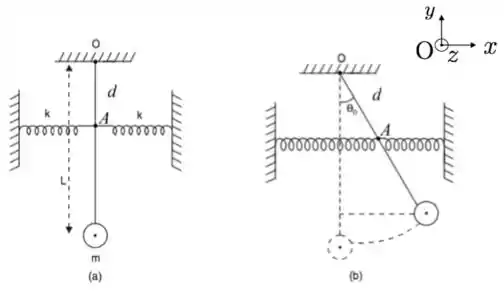
(a) Utilize o sistema de coordenadas da figura e obtenha a equação que descreve o movimento do pêndulo.
(b) Para pequenas oscilações em relação à posição de equilíbrio do pêndulo, determine a freqüência angular de oscilação.
(c) Obtenha a função para pequenas oscilações em relação à posição de equilíbrio.
SUGESTÕES:
• Item (a): Determine o(s) torque(s) em torno ao eixo de rotação ou utilize considerações energéticas.
Passo 1
(a) Como temos uma barra rígida e uma esfera, o sistema é um pêndulo físico. As sugestões dão a dica que a gente pode determinar a equação de movimento usando equação dos torques, ou por energia.
Por torque, basta olharmos todas as forças que agem no sistema e calcular o torque de cada uma delas:
Depois somamos tudo para calcular o torque resultante e aplicamos a segunda lei de Newton para rotações:
Onde e I é o momento de inércia do sistema.
Se preferir calcular por energia , basta somar todas as contribuições energéticas do sistema, cinética rotacional (), potencial gravitacional () e potencial elástica ():
Como todas as forças são conservativas e não há forças externas, a energia se conserva (constante), logo, podemos dizer que
E obter a equação de movimento derivando todos os termos energéticos e igualando a zero.
Vou te mostrar as duas e você escolhe qual você prefere!
Passo 2
- Por Torque
- Por Energia
As forças que agem no pêndulo são o peso da esfera, o peso da haste (desprezível), as duas forças elásticas e a força normal no ponto de sustentação na extremidade superior da haste (ponto O).
Vamos calcular o torque de cada uma em relação ao ponto O, usando .
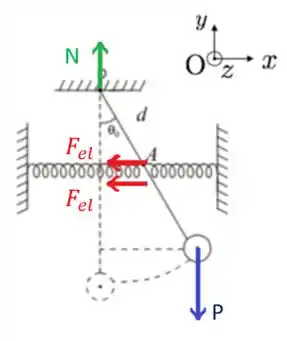
Cada mola exerce uma força elástica , como são duas, multiplicamos por 2
Como a normal está sendo aplicada no ponto de rotação,
Pronto! Temos o torque resultante
Usando a segunda lei de Newton
Como a massa da haste é desprezível e o volume da esfera também, o momento de inércia em relação ao centro de massa é zero, e, pelo teorema dos eixos paralelos
Obtemos a equação diferencial
Se você preferir calcular por energia, vamos calcular cada um dos termos. A energia cinética de rotação vai ser
A energia potencial gravitacional depende da altura da esfera, em . Considerando o zero de energia potencial na altura máxima da esfera, o deslocamento em da esfera será .
A energia potencial elástica, como são duas molas, temos que multiplicar por 2, e o deslocamento das molas, na direção , decompondo, será .
Somando tudo obtemos
Pela conservação de energia
Rearranjando
Como , então
Rearranjando, chegamos na mesma equação de antes
Passo 3
(b) “Para pequenas oscilações”, tá, você já ouviu isso antes, só aproximar o seno e o coseno.
Chegamos em
A solução dessa EDO é um movimento harmônico simples com frequência angular
Passo 4
(c) Para descobrir , temos que lembrar que a solução da EDO acima é um MHS, que pode ser descrito de duas formas (as duas são equivalentes).
Você pode escolher qualquer uma delas, que vai dar no mesmo, eu escolhi a primeira forma
Basta aplicarmos as condições iniciais, que o ângulo inicial é e que a velocidade inicial é nula, para descobrir e
E, derivando,
Juntando tudo, obtemos
Resposta
(a)
(b)
(c)