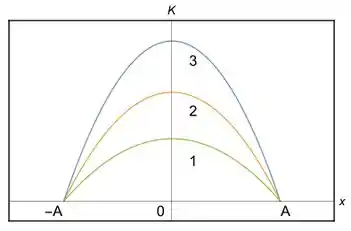
A figura mostra os gráficos da energia cinética K em função da posição x para três osciladores harmônicos do tipo bloco-mola que têm a mesma massa e que descrevem movimentos harmônicos simples. Pode-se dizer que:
(a) A constante elástica do oscilador 2 é maior que a do oscilador 3.
(b) O período de oscilação associado ao oscilador 1 é menor que aquele dos osciladores 2 e 3.
(c) O oscilador 3 completa uma oscilação em um tempo menor que os outros dois.
(d) A constante elástica do oscilador 3 é maior que a dos osciladores 1 e 2, sendo a constante elástica do oscilador 2 menor que a do oscilador 1.
(e) Os três osciladores tem a mesma freqüência de oscilação.
Passo 1
Na teoria vimos que a energia cinética máxima é
E que a energia total em qualquer ponto é sempre
No ponto a mola vai estar relaxada, logo, a energia potencial elástica vai ser zero zero e a energia cinética vai ser máxima.
Pelo gráfico observamos que e sabemos que as massas são iguais.
Vamos analisar as grandezas!
Passo 2
Se a gente juntar as equações acima para o ponto vamos ter que
Como os sistemas tem amplitudes e massas iguais, quanto maior a energia cinética máxima, maior a constante elástica () e maior a frequência angular ().
Isso exclui as alternativas (a) A constante elástica do oscilador 2 é maior que a do oscilador 3, (d) A constante elástica do oscilador 3 é maior que a dos osciladores 1 e 2, sendo a constante elástica do oscilador 2 menor que a do oscilador 1, e (e) Os três osciladores tem a mesma freqüência de oscilação.
Passo 3
Se a gente pensar no tempo de oscilação, o período (T), que é o inverso da frequência:
Quanto maior a frequência angular, menor o período, logo vai ser o inverso da energia cinética máxima:
Isso exclui a alternativa (b) O período de oscilação associado ao oscilador 1 é menor que aquele dos osciladores 2 e 3.
A alternativa correta é (c) O oscilador 3 completa uma oscilação em um tempo menor que os outros dois.
Resposta
(c) O oscilador 3 completa uma oscilação em um tempo menor que os outros dois.