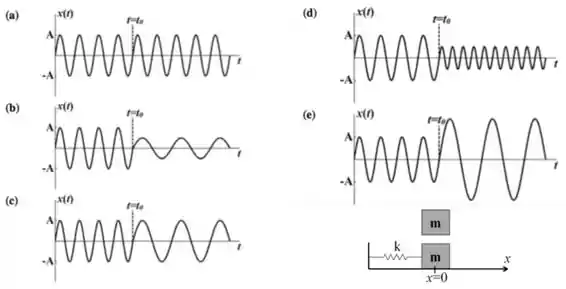
Um oscilador harmônico simples constituído por um bloco de massa m e uma mola de constante elástica realiza um movimento periódico com amplitude em torno da posição de equilíbrio . No instante , o bloco passa pela posição , e no mesmo instante, um outro bloco, de massa m, é solto sobre o primeiro bloco e a nele se fixa. Qual é o gráfico que melhor representa a posição do primeiro bloco em função do tempo?
Passo 1
Nessa questão a gente tem que descobrir duas coisas, se a amplitude e se a frequência mudam após a colisão.
A frequência a gente vai descobrir aplicando diretamente a fórmula, já a amplitude vamos ter que usar conservação de momento linear.
Passo 2
Como a frequência angular só depende da constante elástica e da massa:
Após a colisão, a massa muda para , logo a frequência
A frequência cai, logo a onda vai passar a ter oscilações mais demoradas, o que exclui as alternativas (a) e (d).
Passo 3
Como no ponto a mola está relaxada, a energia potencial elástica (U) é zero, e a energia cinética (K) será máxima. Como o módulo da velocidade máxima pode ser calculada como
A amplitude após a colisão será
Já sabemos a frequência após a colisão, só falta descobrir a depois da colisão (). Vamos usar a conservação de momento linear, antes a massa era e velocidade , após, e velocidade
Jogando na amplitude
Como a amplitude inicial era
A amplitude final será
A amplitude decai por um fator .
A única resposta em que a frequência e a amplitude diminuem é o gráfico (b).
Resposta
(b)