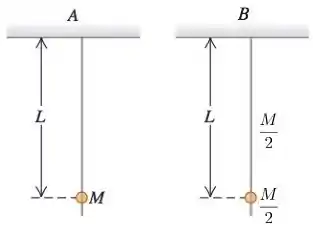
O pêndulo A mostrado na figura consiste em uma esfera muito pequena de massa sustentado por uma corda de massa desprezível e comprimento . O pêndulo B consiste em uma esfera muito pequena de massa e uma barra delgada de massa e comprimento L. Sejam e os tempos que cada pêndulo demora em completar uma oscilação. Para deslocamentos pequenos em relação à posição de equilíbrio, pode-se dizer que:
(a) Os dois pêndulos levam o mesmo tempo para completar uma oscilação, com .
(b) O pêndulo B demora menos tempo que o pêndulo A em completar uma oscilação, com .
(c) O pêndulo B demora menos tempo que o pêndulo A em completar uma oscilação, com
(d) O pêndulo B demora mais tempo que o pêndulo A em completar uma oscilação, com .
(e) O pêndulo B demora mais tempo que o pêndulo A em completar uma oscilação, com .
Formulário:
- Momentos de inércia de uma barra delgada de massa M e comprimento L em relação a um eixo que passa perpendicularmente:
- Teorema dos eixos paralelos: .
– Pelo centro de massas da barra: .
– Por uma das extremidades da barra: .
Passo 1
Como o pêndulo A é muito pequeno, logo ele é um pêndulo simples, com período
Já B é um pêndulo físico, logo o período vai ser
Onde I é o momento de inércia e d é a distância do centro de massa ao ponto onde o pêndulo está preso.
Passo 2
Vamos calcular a posição do centro de massa do sistema em relação ao ponto onde o pêndulo está preso.
Como a esfera (massa ) está a uma distância do eixo de rotação e a barra (massa ) tem seu centro a uma distância , o centro de massa do sistema é
Passo 3
Vamos calcular o momento de inércia do sistema. Basta somar (lembre que a massa tanto da barra quanto da esfera é )
Usando as informações do formulário,
Como a esfera é muito pequena, consideramos seu momento inércia em relação ao centro de massa desprezível, logo, pelo teorema dos eixos paralelos
Passo 4
Substituindo em
Comparando com
Resposta
(b) O pêndulo B demora menos tempo que o pêndulo A em completar uma oscilação, com .