USP – Física 2 – 2019 – P2 – Exercício 2
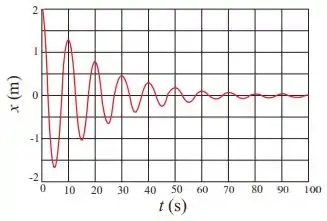
O gráfico abaixo representa a posição de uma partícula em função do tempo , para um oscilador harmônico amortecido. A amplitude inicial , em , e a frequência angular em , desse oscilador são, respectivamente, dadas por:
a) e .
b) e .
c) e .
d) e .
e) e .
Passo 1
Eai galerinha, partiu fazer mais uma questão de prova?
Esse é um exercício bem tradicional: ele fornece o gráfico de um oscilador harmônico amortecido em regime subcrítico e quer a identifiquemos alguns parâmetros. Para isso, temos que lembrar a equação geral da posição nessa situação é do tipo
em que é a amplitude inicial e é a frequência.
Passo 2
Achar a amplitude inicial é bem fácil: basta olhar o ponto de máximo inicial do gráfico e obtemos
Mas cuidado, tem uma pegadinho no enunciado, ele quer a amplitude em :
Passo 3
Para achar a frequência, vamos procurar primeiro o período no gráfico. Vemos que ele completa uma oscilação completa em :
Para achar a frequência angular, lembramos que
Assim,
Portanto,
Assim, caímos na alternativa E 😉
Resposta
Alternativa E.