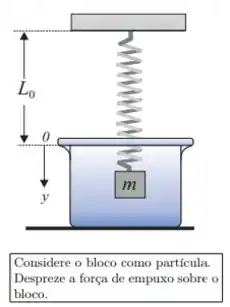
Uma mola de massa desprezível, comprimento e constante se encontra presa ao teto. Na sua extremidade livre é pendurado um bloco de massa . O sistema é abandonada em um meio viscoso cujo coeficiente de atrito viscoso é , sob a ação da força peso (), da força da mola e da força viscosa (). A função que descreve a posição do bloco no tempo, , deste distema será escrita como:
onde é a solução particular (ou estacionária) da equação não-homogênea e é a solução da equação diferencial homogênea. Adotando o eixo como está indicado na figura, resolva as questões Q5, Q6, Q7 e Q8.
Q8) Uma vez que no instante a posição do bloco é e a sua velocidade , determine a solução geral . Resolva de forma literal, sem fazer substituições numéricas.
Passo 1
Antes de qualquer coisa, é importante saber que essa questão é continuação das questões 5, 6 e 7 da P2 de 2019! Na questão 5, obtivemos que a equação diferencial do problema é
Já na questão 6, achamos que a solução particular da equação não-homogênea é
Por fim, na questão 7 identificamos que o regime de oscilação é subcrítico, de modo que a solução geral da equação homogênea é
onde
Passo 2
Desta forma, basta somar com para acharmos a solução geral do problema:
Assim,
Temos que determinar as constante e com as condições iniciais!
Sabemos que para , :
Vamos guardar essa equação.
Passo 3
Derivando a posição com relação ao tempo encontramos a velocidade:
Assim, aplicando a regra do produto:
Ou ainda,
Mas como em também temos , segue que
Com isso, temos duas equações:
Passo 4
Da primeira equação, tiramos
Substituindo na segunda:
Da relação fundamental trigonométrica:
Tiramos:
Assim,
Logo,
Portanto,
Substituindo de volta na equação do cosseno:
Obtemos
Assim, a solução geral do problema é
com
E assim terminamos o problema 😊