Uma mola de massa desprezível, comprimento e constante se encontra presa ao teto. Na sua extremidade livre é pendurado um bloco de massa . O sistema é abandonada em um meio viscoso cujo coeficiente de atrito viscoso é , sob a ação da força peso (), da força da mola e da força viscosa (). A função que descreve a posição do bloco no tempo, , deste distema será escrita como:
onde é a solução particular (ou estacionária) da equação não-homogênea e é a solução da equação diferencial homogênea. Adotando o eixo como está indicado na figura, resolva as questões Q5, Q6, Q7 e Q8.
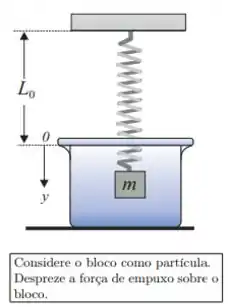
Q5) Escreva a equação diferencial que descreve o movimento deste oscilador, explicitando os valores numéricos dos coeficientes no sistema MKS.
Q6) Determine a solução particular da equação diferencial não-homogênea.
Q7) O movimento do oscilador descrito pela equação homogênea é crítico, subcrítico ou supercrítico? Justifique sua resposta numericamente.
Q8) Uma vez que no instante a posição do bloco é e a sua velocidade , determine a solução geral . Resolva de forma literal, sem fazer substituições numéricas.
Passo 1
Fala pessoal, vamos resolver esse exercício sobre movimento harmônico amortecido. Nessa resolução vamos fazer apenas a Q5, as demais ficam para as resoluções seguintes!
As forças que agem sobre o corpo de massa são: força peso ), força da mola e força viscosa (). Assim, a força resultante é dada pela soma de todas as forças:
Portanto,
Mas pela segunda lei de Newton, sabemos que
Assim,
Essa equação pode ser reescrita como
Passo 2
Dividindo toda a equação por :
Para simplificar um pouco a expressão, renomeamos algumas variáveis:
Assim,
Essa é quase a equação que você está acostumando, tirando aquele do lado direito.
Passo 3
Agora vamos substituir os valores numéricos:
Com , a equação fica
Essa é a resposta da pergunta!