USP – Física 2 – 2019 – P2 – Exercício 7
Uma mola de massa desprezível, comprimento e constante se encontra presa ao teto. Na sua extremidade livre é pendurado um bloco de massa . O sistema é abandonada em um meio viscoso cujo coeficiente de atrito viscoso é , sob a ação da força peso (), da força da mola e da força viscosa (). A função que descreve a posição do bloco no tempo, , deste distema será escrita como:
onde é a solução particular (ou estacionária) da equação não-homogênea e é a solução da equação diferencial homogênea. Adotando o eixo como está indicado na figura, resolva as questões Q5, Q6, Q7 e Q8.
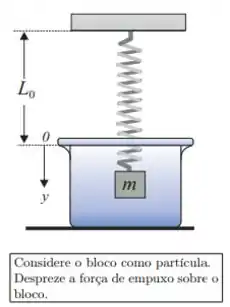
Q7) O movimento do oscilador descrito pela equação homogênea é crítico, subcrítico ou supercrítico? Justifique sua resposta numericamente.
Passo 1
Antes de qualquer coisa, é importante saber que essa questão é continuação das questões 5 e 6 da P2 de 2019! Na questão 5, obtivemos que a equação diferencial do problema é
Substituindo os valores numéricos, encontramos:
Passo 2
Sabemos que o movimento é subcrítico se
É crítica se
E é supercrítico se
Nesse caso,
Portanto, estamos na situação:
Assim, você deve concluir que o regime de oscilação é subcrítico!
Resposta
Movimento subcrítico.