USP – Física 2 – 2019 – P2 – Exercício 4
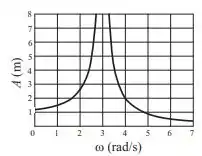
Um sistema de suspensão mecânica ideal de massa e constante elas´tica oscila sem amortecimento, sujeito à força externa da forma . Um estudo demonstra que, quando o sistema atinge o regime estacionário, a amplitude de oscilação do sistema em função da frequência angular da força externa se comporta como na figura ao lado. O valor da constante elástica dos sitema de suspensão é:
a) .
b) .
c) .
d) .
e) .
Passo 1
Fala pessoal, preparados para uma questão sobre movimento harmônico forçado?
O enunciado forneceu um gráfico da amplitude em função da frequência da força externa e quer saber quanto vale a constante elástica da mola. Sabemos que a frequência natural do sistema é dada por
onde a constante da mola e a massa do corpo. Assim,
Passo 2
Para esse tipo de movimento, você deve lembrar que a amplitude é dada por
onde é a amplitude da força externa periódica . Isolando a massa :
Com o gráfico conseguimos achar , pois é a frequência em que a amplitude explode ().
Agora, temos que escolher algum ponto qualquer do gráfico para achar . Note que o melhor ponto para escolher é
Substituindo os valores:
Passo 3
Com isso, já temos e . Portanto,
Logo,
A resposta é alternativa E 😉
Resposta
Alternativa E.