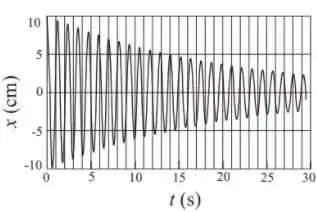
. O gráfico abaixo representa a posição em função do tempo de uma partícula de massa , que realiza um movimento harmônico amortecido, sujeita a uma força onde é a constante de amortecimento e é a velocidade do oscilador. Podemos afirmar que o valor da constante (definida como ) para este movimento é, aproximadamente:
Passo 1
Vem comigo que a gente resolve esse problema!
Como enunciado diz temos um gráfico de um oscilador harmônico amortecido, pelo gráfico temos um caso de amortecimento subcrítico e a amplitude desse movimento é dada por:
Onde é amplitude em , olhando o gráfico vemos que .
Para achar podemos fazer a razão entre em instantes de tempo que temos como saber quanto ele vale.
Para , já temos que:
Olhando o gráfico que em temos que amplitude vale , logo:
Vamos lá então!
Passo 2
Então temos que a razão entre essas duas amplitudes é dada por:
Aplicando nos dois lados, temos:
Mas temos que:
Então temos que:
Usando que , temos que:
Com isso a alternativa correta é a .