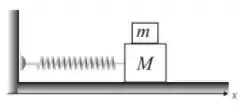
. Um bloco de massa está ligado a uma mola de constante elástica e apóia-se sobre um plano horizontal sem atrito. Um outro bloco, de massa , está no topo do bloco de massa . Se o coeficiente de atrito estático entre os dois corpos é , a distância máxima que os dois corpos podem ser puxados a partir da posição de equilíbrio sem que o bloco de cima escorregue, uma vez que os dois sejam librados é:

Vamos juntos resolver esse problema!

Nosso problema é um caso de oscilação, então a expressão que descreve a posição em função do tempo é dada por:

O enunciado pede o valor máximo de para que o bloco de cima não deslize. A força que mantém o bloco sem deslizar é a força de atrito, então essa força tem que ser maior ou igual a força gerada pela aceleração máxima que o sistema pode adquirir por conta da mola.

A força de atrito máxima é dada por:

A aceleração desse sistema é dada por:

A aceleração máxima acontece quando o cosseno é igual a , então:

Então para o bloco não escorregar temos que:

Então temos que encontrar o valor de para depois achar .