USP – Física 2 – 2019 – P-SUB – M.Escolha
O gráfico mostra a posição em função do tempo de uma partícula de massa , ligada a uma mola de massa desprezível, que move-se em movimento retilíneo, sobre uma mesa horizontal lisa, na direção do eixo x, orientado para a direita.
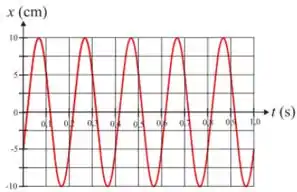
. Podemos afirmar que o instante exato que a partícula estará passando pelo ponto de equilíbrio e movendo-se para a direita, durante o primeiro período do movimento, é:
Passo 1
Vem comigo que juntos a gente resolve essa questão!
Temos uma situação de e o gráfico desse movimento. O enunciado pede o instante em pela primeira vez. Para encontrar esse instante vamos usar a o resultado da questão , temos:
Então temos que ver o valor de para que seja zero.
Passo 2
Vamos lá então, temos:
Para que isso seja verdade temos que:
Então temos que:
Com isso temos que a letra correta é a .